The final launch of the Allmultimedia.org will take place on February 24, 2026
(shortly after the 2026 Winter Olympics).
Geometrie
Z Multimediaexpo.cz

Geometrie (řecky γεωμετρία, z gé - země a metria - měření) je matematická věda, která se zabývá otázkami tvarů, velikostí, proporcí a vzájemných vztahů obrazců a útvarů a vlastnostmi prostorů. Geometrie bývá považována za jeden z nejstarších vědních oborů vůbec. V Ottově slovníku naučném heslo geometrie začíná slovy:
Geometrie, měřičství, jest nauka o veličinách a útvarech prostorových. Pojmů těchto útvarů nabýváme abstrakcí z předmětů hmotných.[1]
Jednoduché geometrické útvary byly známy již v paleolitu a podrobněji zkoumány ve všech antických civilizacích. Geometrie sloužila původně pro praktické účely v zeměměřičství a stavebnictví. Na vědecké úrovni se jim poprvé věnovali staří Řekové. K slavným geometrickým problémům patřili otázky o konstruovatelnosti některých geometrických útvarů pomocí idealizovaného pravítka a kružítka. Ve středověku a raném novověku ovlivnilo studium astronomie rozvoj sférické geometrie a objevení perspektivy v malířství vznik projektivní geometrie. V raném novověku René Descartes vynalezl souřadnice, což umožnilo vznik analytické geometrie a zkoumání geometrie algebraickými prostředky. V 19. století byl významný vznik neeukleidovských geometrií. Geometrie má úzkou souvislost s algebrou a fyzikou. Riemannova geometrie popsaná v 19. století našla uplatnění jako model časoprostoru v Einsteinově obecné teorii relativity. V současnosti se geometrie pořád vyvíjí a to jak geometrie praktická (například počítačová geometrie a počítačová grafika), tak teoretická, která má úzkou souvislost s teoretickou fyzikou. K nejvýznamnějším českým geometrům patřil v první polovině 20. století Eduard Čech. V současnosti je známý matematik Petr Vopěnka, který kromě teoretických prací napsal řadu popularizujících knih o historii geometrie.
Obsah |
Historie
Starověk
Geometrické útvary patří vedle čísel k nejstarším zkoumaným předmětům matematiky, jednoduchou představu o některých z nich měli lidé zřejmě již v paleolitu, starší době kamenné.[2] V neolitu se pak různé útvary staly základem geometrické ornamentiky na více místech světa.[3] Další rozvoj přišel s nástupem prvních států v Mezopotámii a Egyptě, kde se poznatky o útvarech využívaly v zeměměřičství a stavebnictví. Babylóňané již znali zvláštní případy Pythagorovy věty a egyptští geometři uměli počítat obsah trojúhelníka i kruhu, přičemž jejich odhad čísla pí byl asi 3,1605.[3] K řadě poznatků se dospělo také ve starověké Indii a Číně.[4]
Na vědeckou úroveň povznesli matematiku staří Řekové, především Eukleidés, nejznámější geometr starověku. Jeho kniha zvaná Elementy (Στοιχεῖα) se stala na dlouhou dobu základní učebnicí geometrie. Euklides v této knize zachytil abstraktní strukturu geometrických útvarů pomocí definic, axiomů a postulátů. Geometrie vycházející z těchto postulátů se nazývá Euklidovská geometrie a v moderní formě se dnes učí na základních i středních školách. Další geometrické konstrukce známé již ve starověku jsou platónská tělesa (Platón je popsal a uvažoval o jejich hlubším smyslu, zatímco Eukleidés dokázal, že žádná další takto pravidelná tělesa již neexistují), Zénónovy paradoxy o nekonečném dělení úsečky nebo Archimédovy myšlenky o výpočtu objemu těles, předjímající pozdější integrální počet.[5] Geometrie se týkají také tři slavné problémy, které starověká matematika zanechala nevyřešené: trisekce úhlu, zdvojení krychle a kvadratura kruhu.[6]
Středověk
Ve středověku rozvíjeli geometrii především Arabové. Vznikly trigonometrické tabulky a díky arabskému astronomovi al-Battánímu se objevily první poznatky sférické trigonometrie. [7] Arabský filozof a matematik Thabit ibn Qurra v 9. století mimo jiné odvodil vzorec pro zobecněnou Pythagorovu větu, zahrnující i nepravoúhlé trojúhelníky.[8] Mnohé zajímavé geometrické útvary možno najít ve středověké islámské architektuře. Jako dekorace některých staveb se například používala dláždění skládající se z pěti typů dlaždiček (tzv. Giriho dlaždičky), z kterých je podle novějších výzkumů možné sestrojit i neperiodická dláždění.[9] Arabští matematici také uměli algebraicky řešit jisté kubické rovnice a interpretovat výsledky geometricky. [10] V Evropě se v té době na většinu starověkých znalostí zapomnělo a na nově zakládaných evropských univerzitách pak byla používána literatura, která vznikla překladem matematických spisů z arabštiny do latiny, v geometrii hlavně Eukleidových Elementů.[11] V raném novověku rozvoj mechaniky podnítil zájem např. o výpočet těžiště.[12]
Novověk a současnost
V 17. století zavedl Descartes do geometrie souřadnice, čímž položil základy analytické geometrie. Analytická geometrie umožňuje vyjadřovat geometrické útvary prostřednictvím rovnic, a řešit geometrické problémy algebraickou a analytickou cestou.[13] Také to umožnilo zobecnění geometrických úvah na n-rozměrné Eukleidovské prostory i pro n>3. Ke zkoumání geometrických problémů tak bylo možno použít diferenciální a integrální počet, který vznikl díky Newtonovi a Leibnizovi. Paralelní směr vývoje vedl úsilím geometrů jako Desargues, Poncelet, Möbius či Cayley k vytvoření projektivní geometrie, původně motivované teorií perspektivy v malířství. Tato geometrie abstrahuje od pojmu metriky (měření vzdáleností) a stojí pouze na axiomech o bodech a přímkách, které se od Euklidovské geometrie mírně liší (víc odpovídá malířskému plátnu, kde se rovnoběžky "protnou" v nekonečnu).
V 19. století se objevila řada nových proudů a poznatků. Euler a Gauss, Lobačevskij a Riemann popsali první neeuklidovské geometrie, tj. geometrie, ve kterých nemusí existovat jediná rovnoběžka s danou přímkou procházející daným bodem. Tyto konstrukce zároveň ukázaly, že Euklidův pátý postulát je nezávislý na zbylých čtyřech postulátech (nedá se z nich dokázat), což byl v předchozích staletích slavný nevyřešený problém. Riemannova geometrie našla později uplatnění v Einsteinově obecné teorii relativity, kde se fyzikální čas a časoprostor popisuje jako (pseudo)Riemannovská varieta.[14] Évariste Galois popsal počátkem 19. století symetrii polynomů v jedné proměnné a ukázal, že polynom pátého a vyššího stupně není možné obecně řešit pomocí radikálů. Jeho ideje vedly přímo k teorii grup popsané Nielem Henrikem Abelem. Teorie grup umožňuje analyzovat symetrie abstraktním způsobem a práce Evarista Galoise vedla k vyřešení starověkých problémů trisekce úhlu, zdvojení krychle a kvadratury kruhu. Ukázalo se, že tyto konstrukce obecně nelze vytvořit jenom za pomocí pravítka a kružítka. [15] Paralelně s tímto vývojem se od konce 19. století objevují různá axiomatická zavedení geometrie (Hilbert, Tarski, Birkhoff), z nichž nejznámější je Hilbertova axiomatizace.[16] V těchto pojetích se definují základní objekty (obvykle bod, přímka a prostor), relace (například relace bod je mezi dvěma jinými body apod.) a soustava axiomů, ze kterých se dokazují všechna další tvrzení. Další významné nové myšlenky do geometrie přinesl Felix Klein ve vlivném Erlangenském programu v roce 1872. Popsal geometrii pomocí grupy symetrií, které zachovávají nějakou strukturu. Pro Euklidovskou geometrii je to grupa všech posunutí, otočení a zrcadlení, která zachovává vzdálenosti bodů a úhly vektorů. Podle Kleinova přístupu byla každá ze známých geometrií plně charakterizována grupou zachovávající strukturu, která je příslušné geometrii vlastní. Tento přístup vedl ke studiu tzv. Lieových grup, ke kterému výrazně přispěli Sophus Lie a Élie Cartan, který zavedl velmi obecnou definici geometrie, zahrnující všechny tehdy známé geometrické struktury.
Ve 20. století se geometrie nadále vyvíjela více paralelními směry. Geometrie jsou obvykle popisovány jako matematický prostor (hladká varieta nebo topologický prostor) a nějaká další struktura na něm. Převádění těchto struktur, které se často objevují v moderní fyzice, na univerzální Cartanovu definici geometrie, řeší tzv. problém ekvivalence, který se v různých podobách objevuje po celé dvacáté století. Od 50. let je populární podobor geometrie tzv. algebraická geometrie (významnými představiteli jsou například Jean-Pierre Serre a Alexander Grothendieck), která studuje vlastnosti algebraických variet. Přestože je geometrie nejstarší oblastí matematiky, dodnes se vyvíjí. V roce 1995 dokázal Andrew Wiles slavnou velkou Fermatovu větu pomocí teorie eliptických křivek, což je jeden se současných geometrických oborů. Od konce 70. let je v matematice populární Langlandsův program, což je řada hypotéz, které dávají do souvislostí problémy Teorie čísel a reprezentace jistých grup. Geometrická reformulace tohoto programu byla navržena Gérarddem Laumonem a Vladimirem Drinfeldem.[17] Studium geometrických struktur má také úzkou souvislost s řešením parciálních diferenciálních rovnic a problém existence a počtu řešení takových soustav se dá studovat pomocí geometrických metod. [18] Od 80 let 20. století se objevují pokusy studovat problémy pravděpodobnosti a matematické statistiky pomocí metod diferenciální geometrie, což vedlo k zavedení pojmu informační geometrie. [19] V současnosti je také studována tzv. Finslerova geometrie, což je jisté zobecnění Riemannovy geometrie (umíme měřit vzdálenosti, ale úhly vektorů nikoliv). [20] Na přelomu 20. a 21. století definoval Clayův matematický institut sedm tzv. "problémů tisíciletí". Jeden z nich, Hodgeova domněnka, je (zatím nevyřešený) problém z algebraické geometrie. Jiný, Poincarého hypotéza, se týká klasifikace jisté třídy třírozměrných variet a byl (jako zatím jediný) vyřešen v roce 2002 ruským židovským matematikem Perelmanem, který následnou milionovou odměnu i Fieldsovu medaili odmítl.[21]
Členění geometrických oborů
Následuje neúplný seznam nejvýznamnějších a nejznámějších konceptů a podoborů, které se v geometrii vyskytují.
Euklidova geometrie
- Hlavní článek: Euklidova geometrie
Euklidova geometrie se zabývá vlastnostmi a vztahy geometrických útvarů v Euklidově prostoru, t.j. v prostoru, ve kterém platí Euklidovy postuláty. Jedná se o historicky nejstarší geometrii, která byla důkladně popsána a studována už ve starém Řecku. V této geometrii jsou definovány body, přímky, úsečky, kružnice, vzdálenosti bodů a také velikosti a úhly vektorů. Součet úhlů v každém trojúhelníku je 180 stupňů a v pravoúhlých trojúhelnících platí Pythagorova věta. Důležitou částí Euklidovy geometrie jsou konstrukce pravítkem a kružítkem, které se učí na základních a středních školách. Euklidova geometrie se využívá například v počítačové grafice a krystalografii. Slouží také jako fyzikální model prostoru v klasické fyzice a jako teoretický základ deskriptivní geometrie.
Deskriptivní geometrie
- Hlavní článek: Deskriptivní geometrie
Deskriptivní geometrie je věda o zobrazování prostorových útvarů do roviny.[22] Jejím obsahem je popis, jak přesně zakreslit různé prostorové útvary na dvourozměrný papír anebo zobrazit na monitor. Lineární promítací metody byly používány již v Chaldeji (2300 př.n.l.) a starém Egyptě (1200 př.n.l.).[23] Za zakladatele deskriptivní geometrie v dnešním slova smyslu je považován Gaspard Monge (1746-1818), který v díle Géometrie descriptive (1799) popsal kolmé promítání na dvě kolmé průmětny. Metody deskriptivní geometrie se používají například v strojírenství, architektuře, stavebnictví, malířství a kartografii.
Axiomatické geometrie
Axiomatický přístup ke geometrii znamená budovat nějakou teorii z co nejmenšího počtu jednoduchých pravidel (axiomů). Tento přístup stojí v protikladu s geometrií analytickou, která reprezentuje objekty jako množiny bodů. Náznaky se objevily už u Eukleida, který formuloval slavných 5 postulátů. V průběhu 19. století se v souvislosti s objevením neeuklidovkých geometrií Gausse, Lobačevského a Bolyaie obnovil zájem o axiomatizaci těchto struktur. David Hilbert v knize Grundlagen der Geometrie položil základy axiomatické geometrie. Jiný název pro axiomatickou geometrii je syntetická geometrie.
Projektivní geometrie
- Hlavní článek: Projektivní geometrie
Projektivní geometrie[24] může být zadána pomocí axiomů, které se od Euklidovy geometrie liší v tom, že neexistují rovnoběžky a libovolné dvě různé přímky v projektivní rovině se protnou. V této geometrii jsou definovány body a přímky, nikoliv ale úhly a vzdálenosti. Model pro projektivní geometrie je obvykle nějaká projektivní přímka, projektivní rovina, anebo projektivní prostor. Původně byl její vznik inspirován perspektivou v malířství. K rozvoji projektivní geometrie výrazně přizpěli Desargues, Poncelet, Möbius, Cayley a další. V abstraktnějším pojetí studuje projektivní geometrie struktury invariantní vůči projektivním transformacím (homografiím). Invariant vůči takovým transformacím je například dvoupoměr.
Sférická geometrie
- Hlavní článek: Sférická geometrie
Sférická geometrie[25] popisuje geometrii prostoru, který odpovídá sféře (povrchu koule). Je to geometrie metrická, dají se na ní definovat přímky a úsečky jako křivky, které jsou lokálně nejkratší spojnice bodů (tzv. geodetiky). Přímky na sféře jsou všechny hlavní kružnice a libovolné dvě přímky se protnou. Součet úhlů v každém trojúhelníku je větší než 180 stupňů. Sférická geometrie má aplikace v geodezii a astronomii.

Lobačevského geometrie
Lobačevského geometrie,[26] anebo také hyperbolická geometrie, je neeuklidovská geometrie zavedená Bolyaiem a Lobačevským počátkem 19. století. Neplatí v ní pátý Euklidův postulát. Pro přímku a bod, který na ní neleží, existuje v Lobačevského geometrii nekonečně mnoho přímek, které prochází daným bodem a přímku neprotínají. Součet úhlů v trojúhelníku je v této geometrii vždy menší než 180 stupňů. Lobačevského geometrie se dá modelovat například na hyperboloidu, který má zápornou Gaussovu křivost.
Kleinova geometrie
Koncept symetrie se objevuje v geometrii od antiky. Kruh, pravidelný mnohoúhelník a Platónská tělesa vykazují vysokou míru symetrie což vzbuzovalo pozornost řeckých filozofů. Od konce 19. století se objevuje pojetí, že symetrie nějakého objektu (útvar, prostor, geometrie) je jeho charakteristická vlastnost. Popis symetrie je úzce spojen s teorií grup. Toto pojetí je formalizováno v Kleinově Erlangenském programu. Felix Klein v roce 1872 na přednášce v Erlangen definoval geometrii takto:
Geometrie je studium invariantů vůči grupě transformací.[27]
Transformace známých geometrií jsou popisovány pomocí Lieových grup a naopak, studium Lieových grup vedlo k popisu nových geometrických struktur. Geometrie, která je zadána pomocí Lieovy grupy G transformací nějakého prostoru a její význačné podgrupy H, se nazývá Kleinova geometrie.[28] Její zobecnění rozpracoval Élie Cartan.
Diferenciální geometrie
- Hlavní článek: Diferenciální geometrie
Diferenciální geometrie je označení pro geometrické obory, které studují geometrické struktury pomocí metod diferenciálního počtu. Základy diferenciální geometrie položil Carl Friedrich Gauss, který zkoumal vlastnosti křivek a ploch. V modernějším pojetí se diferenciální geometrie zabývá strukturami na hladké varietě. Na ní jsou definovány tečné vektory, vektorová a tenzorová pole, derivace a de Rhamův diferenciál. Geometrie na varietě se obvykle definuje přidáním další struktury (význačná metrika, konexe, diferenciální forma a pod).[29][30]
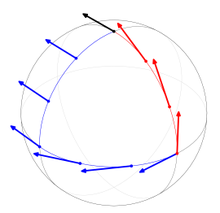
Riemannova geometrie[31] je popsána metrikou na hladké varietě. Je to tedy struktura, na které jsou definovány kromě vektorů i úhly, velikosti vektorů, délky křivek a vzdálenosti. Metrika určuje jednu význačnou beztorzní konexi, díky které je možné přenášet paralelně vektory a definovat geodetiky. V případě, že metrika není pozitivně definitní (tj. některé vektory můžou mít zápornou velikost), mluví se o pseudoriemannově geometrii. Slouží jako model časoprostoru pro Einsteinovu teorii relativity. Symplektická geometrie [32] je popsána antisymetrickou nedegenerovanou uzavřenou diferenciální 2-formou na hladké varietě. Má kořeny v Hamiltonovské formulaci klasické mechaniky a slouží jako model pro fázový prostor jistých klasických systémů. Pokud hybnosti a souřadnice jsou \(p_i, q_i\), forma definující geometrii je \(\sum d p_i \wedge d q_i\). Konformní geometrie [33] je zadána třídou metrik na hladké varietě, které mají tu vlastnost, že v každém bodě jsou stejné až na kladný násobek. Tato struktura nám umožňuje měřit úhly vektorů, nikoliv však vzdálenosti. Analogie přímek jsou tzv. neparametrické geodetiky. Grupa vlastní těmto geometriím je grupa všech transformací, které zachovávají úhly. V komplexní rovině jsou to všechny komplexní holomorfní funkce s nenulovou derivací, ve vyšších dimenzích anebo na sférách je konformních zobrazení podstatně méně. Nejjednodušší model této geometrie je dvourozměrná sféra spolu s množinou všech lineárních lomených transformací (homografií). Cartanova geometrie je velmi obecná definice geometrie a zahrnuje kromě podkladové variety hlavní fibrovaný bundl s nějakou strukturní Lieovou grupou.[28] Na tomto bundlu je definována forma konexe, která ale není afinní, ale tzv. hlavní. Nazývá se Cartanova konexe. Převádění různých klasických geometrických struktur na univerzálnější Cartanovu definic řeší tzv. problém ekvivalence. V poslední době se zkoumá jistá třída Cartanových geometrií, které se nazývají parabolické geometrie.[34] Obsahují a zobecňují projektivní, konformní a symplektickou geometrii, nikoliv ale Riemannovu. Této problematice se v současnosti věnuje několik předních českých matematiků.[35] Diferenciální topologie[36] je věda, která zkoumá topologické (globální) vlastnosti prostorů a zobrazení metodami diferenciální geometrie. Historicky nejstarším příkladem je Gauss-Bonnetova věta, která dává do souvislosti křivost nějakého prostoru a jeho Eulerovu charakteristiku. Modernější příklady jsou Morseho teorie, studium stupně zobrazení, výpočet charakteristických tříd a dalších topologických invariantů, pomocí diferencovatelných funkcí. Další podobory diferenciální geometrie jsou Kontaktní geometrie, Kahlerovské geometrie, CR geometrie, Finslerova geometrie a další.
Algebraická geometrie
- Hlavní článek: Algebraická geometrie
Algebraická geometrie[37] je věda na pomezí geometrie a abstraktní algebry. Studuje vlastnosti polynomů nad obecnými komutativními okruhy, hlavně množinu nulových bodů nějakého systému polynomů. Tyto množiny se nazývají algebraické variety. Podobor algebraické geometrie je studium eliptických křivek, které mají úzkou souvislost s teorií čísel. Aplikace našla teorie eliptických křivek hlavně v kryptografii, [38] ale také v statistice, [39] teorii řízení, [40] geometrickém modelování, [41] teorii strun, [42] teorii her [43] a v dalších oborech.
Geometrická topologie
Geometrická topologie[44] studuje variety a vztahy mezi nimi, například vnoření variet do variet vyšších dimenzí. Předměty studia geometrické topologie jsou například (pořád se vyvíjející) teorie uzlů a topologická klasifikace hladkých variet.
Elementární geometrie
Geometrické útvary
- Hlavní článek: Geometrický útvar
V elementární geometrii se geometrické útvary obvykle reprezentují jako množiny bodů v Euklidově prostoru[45] (případně prvek, jde-li o bod). Rovinné útvary jsou takové útvary, jež leží v rovině. Příklady rovinných útvarů:
- rovinné křivky – např. kuželosečky (kružnice, elipsa, parabola, hyperbola), cykloidy, řetězovky apod.
- trojúhelník, čtyřúhelník a jiné mnohoúhelníky, kruh apod.
Prostorové útvary jsou útvary, které nelze vnořit do roviny. Jsou to například:
- prostorové křivky – např. šroubovice
- plochy v prostoru – např. kvadriky (přímkové plochy, kulová plocha, elipsoid, paraboloid, hyperboloid) apod.
- tělesa – např. mnohostěny (krychle, kvádr, hranol, jehlan), válec, kužel, koule apod.
- Platónská tělesa
Podobně lze uvažovat i vícerozměrné útvary. Příkladem mohou být čtyřrozměrná platónská tělesa. Základní vlastnosti geometrických útvarů jsou například:
- Míry útvarů: délka, obsah, objem, povrch a obvod, jsou-li definovány. Tyto veličiny zjednodušeně řečeno vyjadřují „velikost“ či „rozsah“ útvaru.

- Dimenze: útvarům lze přiřadit číslo, které se nazývá počet rozměrů čili dimenze útvaru. Pro „běžné“ útvary je dimenze celé číslo: pro bod je to nula, pro přímku a obvyklé křivky 1, pro rovinu a běžné zakřivené plochy 2, pro prostorová tělesa jako koule a hranol 3. Existuje více způsobů definice dimenze; podle toho rozlišujeme např. topologickou dimenzi nebo různé fraktální dimenze (jako jsou Hausdorffova míra či Rényiho dimenze), jež pro speciální útvary zvané fraktály mohou být i neceločíselné.[46] (Pro fraktální útvary lze určovat i další speciální vlastnosti, např. lacunaritu,[47] měřící, nakolik fraktál vyplňuje prostor.)
- Symetrie čili souměrnost podle nějakého bodu, přímky či roviny, symetrie vzhledem k otočení nebo zrcadlení, či symetrie vůči změně měřítka (škálovací symetrie). Každému útvaru lze přiřadit jeho grupu symetrií, což je množina všech ortogonálních (případně jiných) zobrazení, které převádí útvar sám na sebe. Existence platónskych těles úzce souvisí s existencí konečných podgrup ortogonální grupy.
- Někdy se užívá pojem otevřený útvar pro útvar, který je otevřený topologicky, tedy obsahuje s každým svým bodem i nějaké jeho okolí. Příkladem je otevřená koule (bez hranice). Podobně se z topologie přebírají pojmy vnitřní body, vnější body, izolované body, hraniční body útvaru a souvislý útvar.
- Uzavřený útvar může znamenat
- Útvar může být konvexní; to znamená, že úsečka mezi libovolnými dvěma jeho body leží celá v útvaru. Z toho je patrné, že konvexní útvar musí být souvislý.
Kromě obecných logických a množinových vztahů (existence, rovnost, inkluze, průnik, sjednocení) se v Euklidovské geometrii také definuje
- Vlastnost „ležet mezi“, např. bod A leží mezi body X a Y na přímce p.
- Shodnost. Dva útvary jsou shodné, pokud existuje otočení, posunutí a zrcadlení (případně jejich kombinace), které jeden útvar zobrazí na druhý. Týká se např. úseček (stejná délka) nebo úhlů (stejná velikost úhlu). Značí se \(\cong\). Například \(\triangle \mathrm{ABC} \cong \triangle \mathrm{DEF}\) čteme „trojúhelník ABC je shodný s trojúhelníkem DEF“ a znamená to, že oba trojúhelníky mají stejné délky stran a velikosti úhlů.
- Podobnost. Dva útvary jsou podobné, pokud mají stejné úhly a proporce, velikosti se ale můžou lišit.
Existují různá matematická zobecnění pojmu geometrický útvar. Topologie se zabývá vlastnostmi množin, které se nemění při spojitých transformacích a topologický prostor je zobecněním pojmu tvar. Vlastnosti útvarů, které se zachovávají při různých transformacích, se nazývají invarianty. V algebraické topologii jsou to například díry různých dimenzí (například kruh bez bodu má díru, plný kruh nikoliv). Invarianty, které formalizují a popisují typy a počty děr, jsou homotopické grupy a homologické grupy[48]
Konstrukce pravítkem a kružítkem
- Hlavní článek: Eukleidovská konstrukce
Konstrukce pomocí kružítka a pravítka označuje konstrukci geometrických objektů (například úhlů) pouze pomocí idealizovaného pravítko a kružítka.[49] O pravítku se předpokládá, ze má nekonečnou délku, jen jednu hranu a žádné značky pro měření, o kružítku se předpokládá, že může nakreslit jakkoli velikou kružnici. Tento pojem se vyskytuje především v zadání úloh, které se týkají konstruovatelnosti. Úkolem bývá určit, zda z daného objektu je možné pomocí pravítka a kružítka vytvořit jiný objekt, který má dané vlastnosti. Příkladem jsou třeba úlohy trisekce úhlu, kvadratura kruhu a duplikace krychle. Lze dokázat, že ani jednu z těchto úloh pomocí Eukleidovské konstrukce vyřešit obecně nelze. V školských úlohách se často objevuje úkol sestrojit trojúhelník s předem danými vlastnostmi.
Analytická geometrie
- Hlavní článek: Analytická geometrie
Analytická geometrie zkoumá geometrické problémy a geometrické útvary popisem jejich souřadnic v pevně zvolené soustavě souřadnic. Popis problému pomocí rovnic pak umožňuje řešit geometrické problémy algebraickými a analytickými prostředky. Geometrické problémy a útvary, které se dají popsat ve vhodně zvolené souřadné soustavě lineární funkcí, jsou předmětem studia lineární algebry. Kuželosečky se v analytické geometrii popisují kvadratickým polynomem ve více proměnných. Za zakladatele analytické geometrie je považován René Descartes, který publikoval základní metody v roce 1637.
Odkazy
Související články
- Dějiny matematiky
- Euklidovská geometrie
- Neeuklidovská geometrie
- Diferenciální geometrie
- Riemannova geometrie
- Deskriptivní geometrie
- Analytická geometrie
- Topologie
Reference
- ↑ Ottův slovník naučný, Geometrie, svazek 10, str. 34, [1]
- ↑ ŠALÁT, Tibor. Malá encyklopédia matematiky. Bratislava : Obzor, 1981. S. 7. (slovensky)
- ↑ 3,0 3,1 Šalát, s. 8
- ↑ Šalát, s. 9
- ↑ Šalát, s. 10–11
- ↑ Šalát, s. 10
- ↑ Šalát, s. 12
- ↑
- ↑
- ↑ KLINE, Morris. Mathematical Thought from Ancient to Modern Times. [s.l.] : Oxford University Press, 1990. 390 s. ISBN 978-0195061352. (anglicky)
- ↑ Miroslav Lávicka, Syntetická geometrie, Pomocný ucební text, ZČU Plzeň, str. 9, dostupné online
- ↑ Šalát, s. 13
- ↑ Šalát, s. 14
- ↑ SCHUTZ, Bernard. A first course in general relativity. [s.l.] : Cambridge University Press, 1985. ISBN 0-521-27703-5. (anglicky)
- ↑ ROTMAN, Joseph. Galois Theory. 2. vyd. [s.l.] : Springer, 1998. 157 s. ISBN 0-387-98541-7. (anglicky)
- ↑ HILBERT, David, The Foundations of Geometry, The Open Court Publishing Company, La Salle, Illinois, 1950, s. 2–15, on-line
- ↑ BUMP & KOL., Daniel. An introduction to the Langlands program. [s.l.] : Birkhäuser, 2003. 283 s. ISBN 3764332115. (anglicky)
- ↑ IVEY, Thomas Andrew; LANDSBERG, Joseph M.. Cartan for beginners. [s.l.] : AMS Bookstore, 2003. ISBN 0-8218-3375-8. (anglicky)
- ↑ HIROSHI, Nagaoka; SHUN-ICHI, Amari. Methods of Information Geometry. [s.l.] : AMS Bookstore, 2007. ISBN 0-8218-0531-2. (anglicky)
- ↑ BAO, David Dai-Wai; CHERN, Shiing-Shen; SHEN, Zhongmin. An introduction to Riemann-Finsler geometry. [s.l.] : Springer, 2000. 431 s. ISBN 0-387-98948-X. (anglicky)
- ↑ . Dostupné online.
- ↑ POMYKALOVÁ, E.. Deskriptivní geometrie pro střední školy. [s.l.] : PROMETHEUS, 2010. ISBN 978-80-7196-400-1. (česky)
- ↑ DRÁBEK, K.; HARANT, F.; SETZER, O.. Deskriptivní geometrie I. [s.l.] : SNTL, 1978. ISBN 80-7083-924-4. S. 9, 10. (česky)
- ↑ COXETER, H.S.M.. Projective Geometry. [s.l.] : Springer, 2003. ISBN 978-0387406237. (anglicky)
- ↑ John C. Polking (Rice University), The Geometry of the Sphere online
- ↑ Milnor, John, Hyperbolic geometry: The first 150 years, AMS, online
- ↑ GALARZA, A.I.R.; SEADE, J.. Introduction to Classical Geometries. [s.l.] : Birkhäuser Basel, 2007. ISBN 978-3764375171. S. 16. (anglicky) , dostupné online
- ↑ 28,0 28,1 SHARPE, R.W.. Differential Geometry: Cartan's Generalization of Klein's Erlangen Program. [s.l.] : Springer, 1997. ISBN 978-0387947327. (anglicky)
- ↑ KOBAYASHI, Shoshichi. Foundations of Differential Geometry. [s.l.] : Wiley-Interscience, 1996. ISBN 978-0471157335. (anglicky)
- ↑ STERNBERG, Sholomo. Lectures on Differential Geometry. [s.l.] : Chelsea Pub Co, 1982. ISBN 978-0828403160. (anglicky)
- ↑ PETERSEN, Peter. Riemannian Geometry. [s.l.] : Springer, 2006. ISBN 978-0387292465. (anglicky)
- ↑ BERNDT, Rolf. American Mathematical Society. [s.l.] : Chelsea Pub Co, 2000. ISBN 978-0821820568. (anglicky)
- ↑ AKIVIS, Maks A.; GOLDBERG, Vladislav V.. Conformal Differential Geometry and Its Generalizations. [s.l.] : Wiley-Interscience, 1996. ISBN 978-0471149583. (anglicky)
- ↑ SLOVAK, Jan; CAP, Andreas. Parabolic Geometries: Background and general theory. [s.l.] : AMS Bookstore, 2009. ISBN 978-0-8218-2681-2. (anglicky)
- ↑ Jan Slovak, publications
- ↑ HIRSCH, Morris W.. Differential Topology. [s.l.] : Springer, 1976. ISBN 978-0387901480. (anglicky)
- ↑ HARTSHORNE, Robin. Algebraic Geometry. [s.l.] : Springer, 2010. ISBN 978-1441928078. (anglicky)
- ↑ Eliška Ochodková, Přínos teorie eliptických křivek k řešení moderních kryptografických systému, Katedra informatiky, FEI, VŠB - Technická Univerzita Ostrava, online
- ↑ DRTON, Mathias; STURMFELS, Bernd; SULLIVANT, Seth. Lectures on algebraic statistics. [s.l.] : Springer, 2009. ISBN 9783764389048. (anglicky)
- ↑ FALB, Peter. Methods of Algebraic Geometry in Control Theory. [s.l.] : Birkhäuser Boston, 1990. ISBN 978-0817634544. (anglicky)
- ↑ JÜTTLER, Bert; PIENE, Ragni. Geometric Modeling and Algebraic Geometry. [s.l.] : Springer, 2007. ISBN 978-3540721840. (anglicky)
- ↑ COX, David A.. Mirror Symmetry and Algebraic Geometry. [s.l.] : AMS, 1999. ISBN 978-0821821275. (anglicky)
- ↑ BLUM, Lawrence E.; ZAME, William R.. The Algebraic Geometry of Perfect and Sequential Equilibrium. Econometrica, Júl 1994, roč. 62, čís. 4. Dostupné online. (anglicky)
- ↑ SHER, R.B.; DAVERMAN, R.J.. Handbook of Geometric Topology. [s.l.] : North Holland, 2002. 1144 s. ISBN 978-0444824325. (anglicky)
- ↑ POLÁK, Josef, Přehled středoškolské matematiky, Praha : Prometheus, 2008, ISBN 978-80-7196-356-1, s. 414
- ↑ VACHTL, Pavel, Fraktály a chaos, Natura, on-line
- ↑ Tolle,C.R. McJunkin,T.R. Rohrbaugh,D.T. a LaViolette,R.A., Lacunarity definition for ramified data sets based on optimal cover, Physica D: Nonlinear Phenomena Volume 179, Issues 3-4, 15 May 2003, s. 129-152. DOI=http://dx.doi.org/10.1016/S0167-2789(03)00029-0
- ↑ .HATCHER, Allen. Algebraic Topology. [s.l.] : Cambridge University Press, 2002. ISBN 0-521-79160-X. (anglicky) Dostupné online
- ↑ Eva Davidová, Řešení planimetrických konstrukčních úloh, Ostrava 2005 (Gymnázium, Ostrava-Poruba), ISBN 80-903647-1-3, dostupné online
Literatura
- VOPĚNKA, Petr. Úhelný kámen evropské vzdělanosti a moci. Praha : Práh, 1999. ISBN 80-7252-022-9. S. 920. (česky)
- VOPĚNKA, Petr. Trýznivé tajemství. Praha : Práh, 2003. 142 s. ISBN 80-7252-088-1. (česky)
- MLODINOW, Leonard. Eukleidovo okno (dějiny geometrie). Praha : SLOVART s. r. o., 2007. ISBN 978-80-7209-900-9. (česky)
- KADEŘÁVEK, František. Geometrie a umění v dobách minulých. Praha : Půdorys, 1997. 140 s. ISBN 80-900791-5-6. (česky)
- BOČEK, Leo; ŠEDIVÝ, Jaroslav. Grupy geometrických zobrazení. Praha : Státní pedagogické nakladatelství, 1979. 213 s. (česky)
- KOWALSKI, Oldřich. Úvod do Riemannovy geometrie. Praha : UK Karolinum, 2003. 101 s. ISBN 80-246-0377-2. (česky)
- COXETER, H.S.M.. Introduction to geometry. [s.l.] : Wiley, 1989. 496 s. ISBN 978-0471504580. (anglicky)
Externí odkazy
- Miroslav Lávička, Syntetická geometrie, Pomocný učební text, ZČU Plzeň
- Ladislav Hlavatý, Úvod do geometrie křivek a ploch, Pomocný učební text, ČVUT Praha
- Jiří Vančura, Apolloniovy úlohy
- Konečný, Zbyněk, Konstrukční úlohy z Planimetrie, SOČ Brno
- Geometrie v Ottově slovníků naučném
- The geometry Jankyard, pokročilé zajímavosti související s geometrií (anglicky)
- Geometrie na mathworld (anglicky)
|
|
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |







