The final launch of the Allmultimedia.org will take place on February 27, 2026
(shortly after the 2026 Winter Olympics).
Trojúhelník
Z Multimediaexpo.cz
Trojúhelník je geometrický útvar, skládající se ze tří vrcholů a tří stran. Pokud leží trojúhelník v Euklidovském prostoru v rovině, je součet velikostí jeho vnitřních úhlů roven 180° (1 π) a libovolné tři body Euklidovské roviny, které neleží na přímce, jsou vrcholy právě jednoho trojúhelníka.
Obsah |
Základní pojmy
Úsečky, které spojují vrcholy, se nazývají strany trojúhelníka. Úhly, které svírají strany, se nazývají vnitřní úhly trojúhelníka. Úhly vedlejší k vnitřním úhlům, se nazývají vnější úhly trojúhelníka. Každý trojúhelník má 3 strany, 3 vnitřní úhly, 6 vnějších úhlů (u každého vrcholu dva). Trojúhelník nemá úhlopříčky.
Znázornění a zápis
Trojúhelník se znázorňuje pomocí jeho vrcholů a stran. Vrcholy se označují velkým tiskacím písmenem, strany se označují malým písmenem příslušným protějšímu vrcholu, úhly se označují malým řeckým písmenem. Trojúhelník se zapisuje symbolem Δ následovaným výčtem všech vrcholů.
Konstrukce trojúhelníku
Trojúhelník může být určen:
- (sss) délkou všech tří stran,
- (sus) délkou dvou stran a velikostí úhlu, který svírají,
- (usu) délkou strany a velikostí úhlů, které k ní přiléhají,
- (Ssu) délkou dvou stran a velikostí úhlu proti větší z nich.
Vlastnosti trojúhelníku
Strany trojúhelníku splňují trojúhelníkové nerovnosti: Součet dvou libovolných stran je vždy delší než strana třetí, neboli
- a + b > c
- a + c > b
- b + c > a , kde a, b, c jsou strany trojúhelníka.
- \(|a - b| < c\)
- \(|b - c| < a\)
- \(|a - c| < b\)
Součet všech vnitřních úhlů je v každém trojúhelníku 180°. Součet vnitřního a příslušného vnějšího úhlu je 180°. Součet dvou vnitřních úhlů se rovná vnějšímu úhlu u zbývajícího vrcholu. Proti většímu úhlu leží větší strana.
- α + α’ = β + β’ = γ + γ’ = 180°
- α + β = γ’
- α + γ = β’
- β + γ= α’
- α + β + γ = 180°
- α’ + β’ + γ’ = 2π
- \(\sin\alpha + \sin\beta + \sin\gamma = 4 \cos\frac{\alpha}{2} \cos\frac{\beta}{2} \cos\frac{\gamma}{2}\)
- \(\cos\alpha + \cos\beta + \cos\gamma = 1 + 4 \sin\frac{\alpha}{2} \sin\frac{\beta}{2} \sin\frac{\gamma}{2}\)
- \(\sin^2\alpha + \sin^2\beta + \sin^2\gamma = 2(1+\cos\alpha \cos\beta \cos\gamma )\)
- \(\cos^2\alpha + \cos^2\beta + \cos^2\gamma = 1 - 2 \cos\alpha \cos\beta \cos\gamma\)
Obecný trojúhelník není osově ani středově souměrný, některé druhy trojúhelníků mohou být osově souměrné. Vztahy mezi úhly a stranami určují sinová, kosinová a tangentová věta. Zavedeme-li veličinu \(s = \frac{1}{2}(a+b+c)\), pak lze velikosti vnitřních úhlů určit ze vztahů
- \(\sin\frac{\alpha}{2} = \sqrt{\frac{(s-b)(s-c)}{bc}}\)
- \(\sin\frac{\beta}{2} = \sqrt{\frac{(s-c)(s-a)}{ac}}\)
- \(\sin\frac{\gamma}{2} = \sqrt{\frac{(s-a)(s-b)}{ab}}\)
- \(\cos\frac{\alpha}{2} = \sqrt{\frac{s(s-a)}{bc}}\)
- \(\cos\frac{\beta}{2} = \sqrt{\frac{s(s-b)}{ac}}\)
- \(\cos\frac{\gamma}{2} = \sqrt{\frac{s(s-c)}{ab}}\)
Druhy trojúhelníků
Podle stran
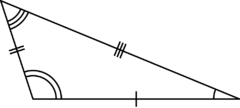
- Obecný trojúhelník (též různostranný) – žádné dvě strany nejsou shodné
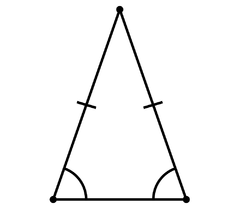
- Rovnoramenný trojúhelník – dvě strany jsou navzájem shodné, ale nejsou shodné s třetí stranou
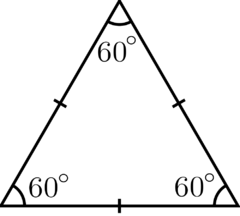
- Rovnostranný trojúhelník – všechny strany jsou shodné
| 
| 
|
| Obecný | Rovnostranný | Rovnoramenný |
|---|
Podle úhlů
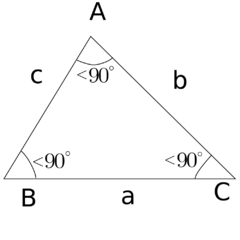
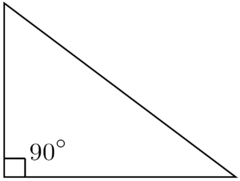
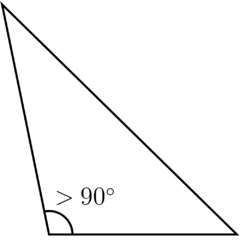
- Ostroúhlý trojúhelník – všechny vnitřní úhly jsou ostré
- Pravoúhlý trojúhelník – jeden vnitřní úhel je pravý, zbývající dva jsou ostré
- Tupoúhlý trojúhelník – jeden vnitřní úhel je tupý, zbývající dva jsou ostré
| 
| 
|
| Ostroúhlý | Pravoúhlý | Tupoúhlý |
|---|
Důležité přímky trojúhelníka
Výška
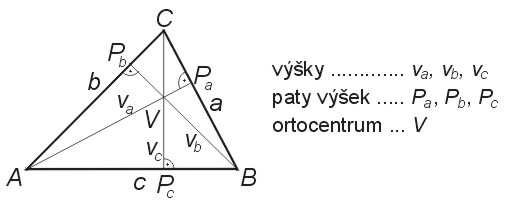
Výška je úsečka, jejímiž krajními body jsou vrchol trojúhelníku a pata kolmice vedené tímto vrcholem na protější stranu. Průsečík výšky s příslušnou stranou se nazývá pata výšky. Každý trojúhelník má tři výšky. Menší straně odpovídá větší výška. Přímky, na nichž leží výšky, se protínají v jednom bodě, který se nazývá ortocentrum. Ortocentrum leží uvnitř trojúhelníka, pokud je ostroúhlý. U pravoúhlého trojúhelníka splývá s jeho vrcholem, při němž je pravý úhel. U tupoúhlého trojúhelníka leží ortocentrum vně. Spojnice jednotlivých pat výšek tvoří ortický trojúhelník. Pravoúhlý trojúhelník svůj ortický trojúhelník nemá, protože jeho dvě paty výšek splývají. Ortocentrum ostroúhlého trojúhelníka je středem kružnice vepsané jeho ortickému trojúhelníku; ortocentrum tupoúhlého trojúhelníka je středem jedné z kružnic připsaných jeho ortickému trojúhelníku. Výšky se označují malým písmenem v s dolním indexem příslušné strany. Pro výšky trojúhelníka platí
- \(v_a:v_b:v_c = \frac{1}{a}:\frac{1}{b}:\frac{1}{c}\)
Velikosti výšek jsou určeny vztahy
- \(v_a = b\sin\gamma = c\sin\beta\)
- \(v_b = a\sin\gamma = c\sin\alpha\)
- \(v_c = a\sin\beta = b\sin\alpha\)
Těžnice
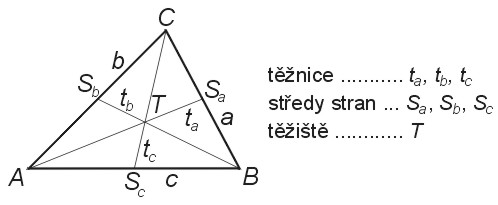
Těžnice je úsečka, jejímiž krajními body jsou střed strany a protilehlý vrchol trojúhelníku. Každý trojúhelník má tři těžnice. Těžnice se protínají v jednom bodě, který se nazývá těžiště. Těžiště rozděluje každou těžnici na dva díly v poměru 2 : 1, přitom vzdálenost těžiště od vrcholu je dvojnásobek vzdálenosti od středu protější strany. Každá těžnice rozděluje trojúhelník na dva díly se stejným obsahem. Těžnice se označují malým písmenem t s dolním indexem příslušné strany, těžiště se označuje písmenem T. Těžiště a dva vrcholy trojúhelníka tvoří postupě tři trojúhelníky (ABT, ACT, CBT), všechny tři mají stejný obsah. Velikost těžnice je dána
- \(t_a = \frac{1}{2}\sqrt{2(b^2+c^2)-a^2}\)
- \(t_b = \frac{1}{2}\sqrt{2(a^2+c^2)-b^2}\)
- \(t_c = \frac{1}{2}\sqrt{2(a^2+b^2)-c^2}\)
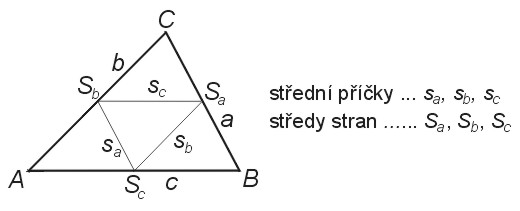
Střední příčka
Střední příčka je spojnice středů dvou stran (dvou pat těžnic). Každý trojúhelník má tři střední příčky. Střední příčka je rovnoběžná s příslušnou stranou a má velikost poloviny příslušné strany. Střední příčky dohromady rozdělují trojúhelník na čtyři shodné trojúhelníky - příčkový trojúhelník a tři trojúhelníky při jednotlivých vrcholech. Těžiště trojúhelníka je zároveň těžištěm jeho příčkového trojúhelníka. Střední příčky se označují malým písmenem s
Symediána
Symediána je osově souměrný obraz těžnice podle osy příslušného úhlu (např. symediána těžnice z vrcholu A podle osy úhlu při vrcholu A). Každý trojúhelník má tři symediány. Všechny symediány trojúhelníka se protínají v jednom bodě, který se nazývá Lemoinův bod. Lemoinův bod leží uvnitř trojúhelníka a platí pro něj, že má ze všech vnitřních bodů trojúhelníka nejmenší součet čtverců vzdáleností od stran trojúhelníka. Pokud Lemoinovým bodem vedeme rovnoběžky s jednotlivými stranami, všechny průsečíky těchto rovnoběžek se stranami (je jich šest) leží na kružnici, která se nazývá první Lemoinova kružnice. Střed první Lemoinovy kružnice je středem úsečky spojující Lemoinův bod a střed kružnice opsané.
Osy úhlů
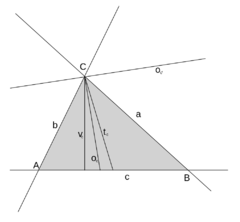
Osa vnitřního úhlu dělí protější stranu v poměru délek přilehlých stran. Osa vnitřního úhlu dělí tento vnitřní úhel na polovinu. Podobně osa vnějšího úhlu dělí vnější úhel na polovinu. Na obrázku je osa vnitřního úhlu \(o_c\), osa vnějšího úhlu \(o_c^\prime\) a také těžnice \(t_c\) a výška \(v_c\) z vrcholu \(C\). Podobně lze získat osy i u ostatních vrcholů.
Třetiny úhlů
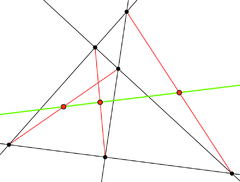
Pokud jednotlivé vnitřní úhly rozdělíme přímkami na tři stejné díly (trisekce úhlu), průsečíky těchto přímek (vždy těch dvou, které jsou bližší dané straně trojúhelníka) vždy tvoří rovnostranný trojúhelník (Morleyova věta).
Osy stran
Osa strany je kolmice vedená ze středu strany. Osy stran se protínají v jednom bodě.
Eulerova přímka
Eulerova přímka je přímka, která prochází těžištěm a ortocentem. Na Eulerově přímce leží i střed kružnice opsané a střed kružnice devíti bodů. V rovnostranném trojúhelníku těžiště a ortocentrum splývají, takový trojúhelník Eulerovu přímku nemá.
Gaussova přímka
Pokud přímka p protíná přímky, na nichž leží strany trojúhelníka, v bodech X, Y, Z, pak středy úseček AX, BY, CZ leží na přímce. Tato přímka se nazývá Gaussova přímka.
Kružnice opsaná, vepsaná a připsaná
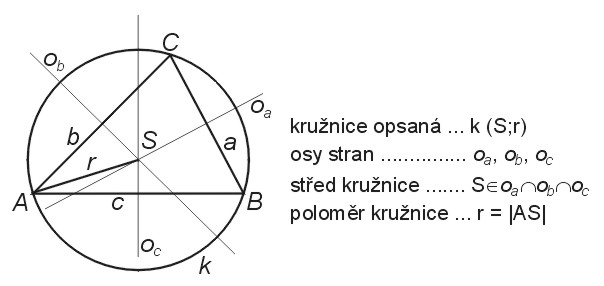
Kružnice opsaná trojúhelníku je kružnice, která prochází všemi vrcholy trojúhelníka. Každému trojúhelníku lze opsat kružnici. Střed kružnice opsané leží v průsečíku os stran, poloměr se rovná vzdálenosti středu od libovolného vrcholu. Spojnice středu kružnice opsané a jednotlivých vrcholů trojúhelníka jsou kolmé k jednotlivým stranám jeho ortického trojúhelníka (tzv. Nagelova věta). Velikost poloměru opsané kružnice určuje vztah
- \(r = \frac{a}{2\sin\alpha} = \frac{b}{2\sin\beta} = \frac{c}{2\sin\gamma}.\)
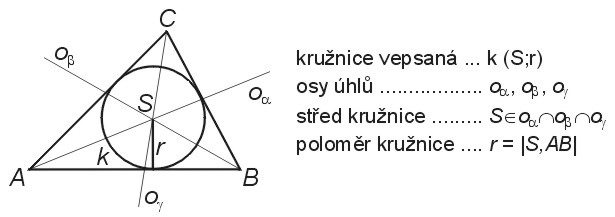
 Kružnice vepsaná trojúhelníku je kružnice, která se dotýká všech stran trojúhelníka. Každému trojúhelníku lze vepsat kružnici. Střed kružnice vepsané leží v průsečíku os vnitřních úhlů, poloměr se rovná kolmé vzdálenosti středu od libovolné strany.
Pro poloměr kružnice vepsané platí
Kružnice vepsaná trojúhelníku je kružnice, která se dotýká všech stran trojúhelníka. Každému trojúhelníku lze vepsat kružnici. Střed kružnice vepsané leží v průsečíku os vnitřních úhlů, poloměr se rovná kolmé vzdálenosti středu od libovolné strany.
Pro poloměr kružnice vepsané platí
- \(\rho = \frac{1}{2}(a+b+c) \operatorname{tg}\frac{\alpha}{2} \operatorname{tg}\frac{\beta}{2} \operatorname{tg}\frac{\gamma}{2} = \frac{S}{s}.\)
 Vzdálenost mezi středy kružnice vepsané a opsané je
Vzdálenost mezi středy kružnice vepsané a opsané je
- \(d = \sqrt{r^2 - 2r\rho}.\)
Kružnice připsaná trojúhelníku je kružnice, která se dotýká jedné strany trojúhelníka a dvou přímek, které jsou prodloužením zbývajících stran trojúhelníka. Střed kružnice připsané leží v průsečíku osy jednoho vnitřního úhlu a dvou vnějších úhlů při zbývajících dvou vrcholech. Každý trojúhelník má tři kružnice připsané.
Obvod a obsah
Obvod trojúhelníku o se vypočte jako součet všech jeho stran:
- o = a + b + c , kde a, b, c jsou strany trojúhelníku
Obsah trojúhelníku S se vypočte jako polovina součinu libovolné strany a k ní příslušné výšky:
- S = z . v / 2 , kde v je výška příslušná straně z
Pokud není známá příslušná výška, je možné obsah trojúhelníku vypočítat podle Heronova vzorce
- s = o / 2 kde o je obvod trojúhelníku
- S = \(\sqrt{s(s-a)(s-b)(s-c)}\)
Obsah trojúhelníku pomocí poloměru kružnice opsané (\(r\)):
- \(S=\frac{abc}{4r}=2r^2 \sin\alpha\sin\beta\sin\gamma\)
Obsah trojúhelníku pomocí poloměru kružnice vepsané (\(\rho\)):
- \(S=\frac{a+b+c}{2}\rho\)
Obsah trojúhelníku pomocí vnitřního úhlu:
- \(S=\frac{1}{2}ab\,\sin\gamma=\frac{1}{2}ac\,\sin\beta=\frac{1}{2}bc\,\sin\alpha\)
Obsah obecného trojúhelníku v rovině kde (ax,ay), (bx,by), (cx,cy) jsou souřadnice vrcholů (vychází z vektorového součinu, použití hlavně v grafice):
- \(S=\frac{1}{2}|(c_x - a_x)(b_y - a_y) - (c_y - a_y)(b_x - a_x)|\)
nebo:
- \(S=\frac{1}{2}|[a_x (c_y - b_y) + b_x(a_y - c_y)+c_x(b_y - a_y)]|\)
Použije-li se předcházející vzorec bez absolutní hodnoty, lze jej využít pro ověření zda bod (dx;dy) leží uvnitř trojúhelníka ABC. V případě, že leží, tak znaménka ploch všech čtyř trojúhelníků ABC, ABD, BCD a CAD jsou stejná. Leží-li vně, nemají všechny plochy stejné znaménko.
Věty o trojúhelníku
V trojúhelníku platí všelijaké věty, vzorce, poučky. Např.
- sinová věta
- kosinová věta (zobecnění Pythagorovy věty na nepravoúhlý trojúhelník)
- tangentová věta
V pravoúhlém trojúhelníku navíc:
Související články
Literatura
- ŠVRČEK, Jaroslav; VANŽURA, Jiří. Geometrie trojúhelníka. Praha : Nakladatelství technické literatury, 1988.
Externí odkazy
- Výpočet úhlů a stran pravoúhlého trojúhelníku
- Základní konstrukce v trojúhelníku - flashová animace sestrojení výšek, těžnic, kružnic opsané a vepsané
|
|
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |