Vektor

Z Multimediaexpo.cz

Vektor představuje ve fyzice a vektorovém počtu veličinu, která má kromě velikosti i směr. Tím se liší od obyčejného čísla, neboli skaláru, které má pouze velikost. Příkladem vektoru je síla — má velikost a směr, a více sil se skládá dohromady podle zákona o skládání sil - rovnoběžníkového pravidla. Vektory se ve fyzice obvykle popisují pomocí souřadnic, které ovšem závisí na volbě souřadnicových os. V matematice je někdy definován vektor jako uspořádaná n-tice prvků (typicky čísel), označovaných jako složky (též komponenty) vektoru. Obecněji se vektor dá chápat jako abstraktní prvek vektorového prostoru. Prvek vektorového prostoru se dá v různých souřadnicích vyjádřit různými n-ticemi, které se však považují za ten samý vektor. Počet složek vektoru souvisí s dimenzí vektorového prostoru.

Obsah [skrýt] 1 Definice 1.1 Pravý a axiální vektor 2 Reprezentace vektoru 3 Operace s vektory 3.1 Sčítání vektorů 3.2 Násobení vektoru číslem 3.3 Součin vektorů 3.4 Vlastnosti vektorových operací 3.5 Invariance operací 3.6 Další vektorové operace 4 Druhy vektorů 4.1 Jednotkový vektor 4.2 Nulový vektor 4.3 Tečný vektor 4.4 Hermiteovsky sdružený vektor 5 Související články

Definice

Neformálně je vektor veličina charakterizovaná velikostí (v matematice číslem, ve fyzice počtem jednotek) a směrem. Často je reprezentovaná graficky jako šipka. Příkladem je „Pohyb na sever rychlostí 90 km/hod“ nebo „Přitahován ke středu Země silou 70 newtonů“. Ve fyzice se vektory obvykle zapisují v souřadnicích. Aby byl vektor dobře definován, požaduje se následující vlastnost: jestliže si zvolím novou souřadnicovou soustavu a měřím body v prostoru v novém souřadném systému, pak souřadnice vektoru se změní podle stejného vzorce jak souřadnice bodů v prostorů. Tato vlastnost se nazývá invariance vůči změně souřadnic. Tedy jestliže systém souřadnic podstoupí lineární transformaci popsanou vztahem $x_i^{\prime }=\sum _{j=1}^n{a}_{ij}{x}_j$, pak složky libovolného vektoru $\mathbf{v}$ se podobně transformují podle vztahu

$v_i^{\prime }=\sum _{j=1}^n{a}_{ij}{v}_j$,

kde $v_i$ jsou složky vektoru $\mathbf{v}$ v původní soustavě souřadnic a $v_i^{\prime }$ jsou složky vektoru $\mathbf{v}$ v nové soustavě souřadnic. Tuto transformaci lze vyjádřit v maticovém zápisu jako ${\mathbf{v}}^{\prime }=\mathbf{A}\cdot \mathbf{v}$, kde $\mathbf{A}$ je transformační matice se složkami $a_{ij}$. Někdy se požaduje invariance ne vůči všem lineárním transformacím, ale jen rotacím a zrcadlením (v klasické mechanice), nebo Lorentzovým transformacím (v speciální relativitě). Pokud není vektor vázán k žádnému pevnému bodu prostoru, tzn. pro jeho vyjádření je důležitý pouze jeho směr a velikost, pak hovoříme o volném vektoru. Pokud je daný vektor spojen s určitým bodem prostoru (t.j. má počátek), pak hovoříme o vázaném vektoru. Vektory mohou být shodné $(x_i)=(x_i)$ (tj. mají stejnou velikost a stejnou orientaci) a nebo opačné (tj. $(-x_i)$ je stejný vektor ale s opačným směrem než vektor $(x_i)$) Pokud je vektor definován v každém bodě prostoru, pak se hovoří o vektorovém poli. V matematice se pod pojmem vektor obvykle rozumí prvek nějakého vektorového prostoru. Tyto prostory můžou být i nekonečněrozměrné, proto někdy má smysl mluvit, že i funkce je vektor, anebo stav fyzikálního systému je vektor (v kvantové mechanice).

Pravý a axiální vektor

Jako pravý vektor označujeme takovou vektorovou veličinu, která se dá nějakým způsobem měřit nebo počítat za předpokladu pevně zvolené ortonormální souřadnicové soustavy a když se podle stejných pravidel změří nebo spočte v souřadnicové soustavě, která je vůči původní otočená nebo zrcadlená, vyjde nám „stejný“ vektor (t.j. jeho souřadnice se vůči původním změnily podle stejného vzorce než souřadnice bodů v prostoru). Při zrcadlení os tedy pro pravý vektor platí

$\mathbf{V}(-x_i)=\mathbf{V}(x_i),$

kde $(-x_i)$ označuje souřadnicovou soustavu, která má opačnou orientaci jako $(x_i)$ . Vektorovou veličinu, která se při rotacích transformuje stejně jako souřadnice, avšak při zrcadlení souřadnicových soustav mění znaménko, označujeme jako axiální vektor (nepravý vektor nebo pseudovektor). Při zrcadlení os tedy pro axiální vektor platí

$\mathbf{V}(-x_i)=-\mathbf{V}(x_i).$

Matematicky se dá axiální vektor definovat jako prvek druhé vnější mocniny prostoru (v dimenzi 3), resp. obecněji jako prvek (n-1)-ní vnější mocniny ${\wedge }^{n-1}\mathbf{V}$ n-rozměrného vektorového prostoru V. Za předpokladu volby skalárního součinu a orientace na V pak můžeme takový prvek ztotožnit s vektorem (prvkem V) pomocí Hodgeovy duality. Znaménko výsledného vektoru pak závisí na volbě orientace. Příkladem pravého vektoru je polohový vektor $\mathbf{r}$ nebo vektor rychlosti $\mathbf{v}$, axiálním vektorem je např. vektor úhlové rychlosti $\mathbf{\Omega }$. Pseudovektory se často konstruují z pravých vektorů pomocí vektorového součinu (je invariantní vůči rotacím, ale ne zrcadlením).

Reprezentace vektoru

Symboly pro vektory jsou obvykle tištěny tučně, jako a; to je také konvence použitá v této encyklopedii. Mezi další zvyklosti označování patří $\overrightarrow{a}$ nebo a, zvlášť při ručním psaní. Alternativně lze použít i ã.

Vektory se obvykle v grafech nebo jiných diagramech označují jako šipky, jak je znázorněno na obrázku :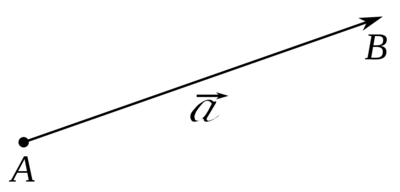

Zde bod A se nazývá báze nebo počátek; bod B se nazývá hlava, vrchol, koncový bod, nebo cíl. Délka šipky představuje velikost vektoru, směr šipky představuje směr vektoru. Vektory jsou také často vyjadřovány pomocí svých složek, např. $a_i$ pro vektor $\mathbf{a}$. V pokročilejší matematické či fyzikální literatuře se pro vektory žádné speciální značení nepoužívá a jsou označovány stejně jako ostatní veličiny, popř. se používá složkový zápis. Např. místo $\mathbf{a}$ se použije $a_i$ nebo pouze $a$. Kvantová fyzika používá pro zápis vektoru tzv. Diracovu symboliku. V diferenciální geometrii se vektor v dané souřadné soustavě často vyjadřuje pomocí operátorů parciálních derivací, tedy např. jako

$\mathbf{A}=a_x\frac{\mathit{\partial }}{\mathit{\partial }x}+a_y\frac{\mathit{\partial }}{\mathit{\partial }y}+a_z\frac{\mathit{\partial }}{\mathit{\partial }z}.$

S výhodou se využívá faktu, že při obecných transformacích souřadnic se vektory transformují stejně jako parciální derivace - pomocí řetízkového pravidla.

Operace s vektory

Sčítání vektorů

Pro dva vektory $\mathbf{A},\mathbf{B}$ ze stejného vektorového prostoru je definován jejich součet $\mathbf{C}=\mathbf{A}+\mathbf{B}$. Pro složky vektorů platí $C_i=A_i+B_i$ Pokud jsou dva vektory na sebe kolmé, lze velikost výsledného vektoru určit Pythagorovou větou. Výsledný vektor je možno reprezentovat graficky a to doplněním do vektorového rovnoběžníku (nechť je cíl výsledného vektoru bod C, počátek bod A, cíl vektoru 1 bod B a cíl vektoru 2 bod D. Úhlopříčka AC vektorového rovnoběžníku ABCD pak představuje výsledný vektor. Délka této vektorové úsečky je rovna velikosti výsledného vektoru.)

Násobení vektoru číslem

Pro libovolný vektor $\mathbf{A}$ a číslo $k$ je definován vektor $k\mathbf{A}$ se složkami

$k\cdot A_i$.

Součin vektorů

Součin vektorů lze definovat různým způsobem. Používané součiny vektorů jsou

• tenzorový součin
• skalární součin
• vektorový součin
• smíšený součin
• dvojitý vektorový součin

Vlastnosti vektorových operací

Mějme vektory $\mathbf{A},\mathbf{B},\mathbf{C}$ a skaláry $a,b$. Pak platí komutativní zákon pro sčítání vektorů

$\mathbf{A}+\mathbf{B}=\mathbf{B}+\mathbf{A}$

Pro sčítání dvou vektorů platí asociativní zákon, tzn.

$\mathbf{A}+(\mathbf{B}+\mathbf{C})=(\mathbf{A}+\mathbf{B})+\mathbf{C}$

Platí také asociativní zákon pro násobení číslem, tedy

$a(b\mathbf{A})=(ab)\mathbf{A}$

Dále platí distributivní zákony

$(a+b)\mathbf{A}=a\mathbf{A}+b\mathbf{A}$

$a(\mathbf{A}+\mathbf{B})=a\mathbf{A}+a\mathbf{B}$

Existuje nulový vektor $\mathbf{0}$ splňující následující vztahy

$\mathbf{A}+\mathbf{0}=\mathbf{A}$

$\mathbf{0}\cdot \mathbf{A}=\mathbf{0}$

$a\mathbf{0}=\mathbf{0}$

Ke každému vektoru $\mathbf{A}$ existuje opačný vektor $-\mathbf{A}$, pro nějž platí

$\mathbf{A}+(-\mathbf{A})=\mathbf{0}$

$-(a\mathbf{A})=(-a)\mathbf{A}=a(-\mathbf{A})$

Pokud $\mathbf{B}=\mathbf{A}+\mathbf{C}$, pak

$\mathbf{C}=\mathbf{B}+(-\mathbf{A})=\mathbf{B}-\mathbf{A}$

Za lineární kombinaci dvou vektorů $\mathbf{A},\mathbf{B}$ je považován vektor $\mathbf{C}=a\mathbf{A}+b\mathbf{B}$, kde a, b jsou libovolná čísla, jehož složky jsou

$C_i=a{A}_i+b{B}_i$

Dva lineárně závislé vektory označujeme jako kolineární (rovnoběžné). Jsou-li dva vektory lineárně závislé, je jeden z nich násobkem druhého, oba tedy určují stejný směr v prostoru a jsou tedy rovnoběžné. Vektorový součin dvou kolineárních vektorů v ${\mathbb{R}}^3$ je nulový. Tři vzájemně lineárně závislé vektory označujeme jako komplanární. Komplanární vektory leží v jedné rovině. Smíšený součin komplanárních vektorů v ${\mathbb{R}}^3$je nulový. Pro součiny vektorů v ${\mathbb{R}}^3$ platí důležité vztahy, jako je např. jacobiho identita pro dvojitý vektorový součin, tzn.

$\mathbf{A}\times (\mathbf{B}\times \mathbf{C})+\mathbf{B}\times (\mathbf{C}\times \mathbf{A})+\mathbf{C}\times (\mathbf{A}\times \mathbf{B})=0$

Dále tzv. Lagrangeova identita

$(\mathbf{A}\times \mathbf{B})\cdot (\mathbf{C}\times \mathbf{D})=(\mathbf{A}\cdot \mathbf{C})(\mathbf{B}\cdot \mathbf{D})-(\mathbf{A}\cdot \mathbf{D})(\mathbf{B}\cdot \mathbf{C})$

Speciálním případem Lagrangeovy identity je vztah

${(\mathbf{A}\times \mathbf{B})}^2={\mathbf{A}}^2{\mathbf{B}}^2-{(\mathbf{A}\cdot \mathbf{B})}^2$

Dalšími často užívanými vztahy jsou

$(\mathbf{A}\times \mathbf{B})\times (\mathbf{C}\times \mathbf{D})=[\mathbf{A}(\mathbf{B}\times \mathbf{D})]\mathbf{C}-[\mathbf{A}(\mathbf{B}\times \mathbf{C})]\mathbf{D}$

$\mathbf{A}\times [\mathbf{B}\times (\mathbf{C}\times \mathbf{D})]=(\mathbf{A}\times \mathbf{C})(\mathbf{B}\cdot \mathbf{D})-(\mathbf{A}\times \mathbf{D})(\mathbf{B}\cdot \mathbf{C})$

Invariance operací

Sčítání vektorů je invariantní vůči všem lineárním zobrazením, t.j. $\mathbf{A}(\mathbf{x}+\mathbf{y})=\mathbf{A}\mathbf{x}+\mathbf{A}\mathbf{y}$ pro nějakou lineární transformaci A, přičemž x a y označují vektory. Vektorový součin dvou vektorů z ${\mathbb{R}}^3$ je invariantní vůči rotacím (ale ne zrcadlením). To znamená $\mathbf{A}(\mathbf{v}\times \mathbf{w})=\mathbf{A}(\mathbf{v})\times \mathbf{A}(\mathbf{w})$ pro libovolnou rotaci A. Znamená to, že vektorový součin je dobře definován i na abstraktním třírozměrném reálném vektorovém prostorů, pokud je na něm definován skalární součin a orientace. Vektorový součin dvou vektorů v prostoru je tedy dobře definován i „fyzikálně“, až na znaménko (je to pseudovektor). Skalárni součin je invariantní vůči všem rotacím, ale navíc i zrcadlením (a nejen u třirozměrných reálných prostorových vektorů, ale i obecně.) Smíšený součin tří vektorů z ${\mathbb{R}}^3$ je invariantní vůči všem lineárním zobrazením, které zachovávají objem a nemění orientaci prostoru (množina takových zobrazení se standardně značí $SL(3)$). Znamená to opět, že při dané volbě orientace (fyzikálního) třírozměrného prostorů je smíšený součin 3 vektorů dobře definován, obecně jeho znaménko závisí na orientaci prostoru (je to pseudoskalár).

Další vektorové operace

Operace na vektorech:

• norma vektoru
• gradient vektorového pole
• divergence
• rotace

Druhy vektorů

Jednotkový vektor

Jednotkovým vektorem označujeme vektor e s jednotkovou normou, tzn. $|\mathbf{e}|=1$. Jednotkový vektor ve směru libovolného vektoru $\mathbf{V}$ je určen vztahem

$\mathbf{e}=\frac{\mathbf{V}}{|\mathbf{V}|}$

Nulový vektor

Nulový vektor $\mathbf{0}$ je zvláštním případem vektoru, který lze zapsat jako uspořádanou n-tici $(0,0,\cdots ,0)$, tzn. všechny složky vektoru jsou nulové. Norma nulového vektoru je rovna nule. Z hlediska fyzikálního nemá nulový vektor směr ani orientaci.

Tečný vektor

Je vektor vyskytující se na varietách, který má počátek (t.j. pevný bod, z kterého vychází) a určuje rychlost pohybujícího se objektu, který daným bodem prochází. (Formálně se definuje tak, že hladké funkci přiřadí příslušnou směrovou derivaci). Ve fyzice se často pracuje s vektorovými poli na varietách.

Hermiteovsky sdružený vektor

Vektor je obvykle vyjadřován jako sloupec s komponentami

$\left(\begin{array}{c}{a}_1\\ a_2\\ ⋮\\ a_n\end{array}\right)$

Hermiteovské sdružení představuje aplikaci transpozice a komplexního sdružení, čímž získáme hermiteovsky sdružený vektor se složkami

$(a_1^{\ast },a_2^{\ast },\cdots ,a_n^{\ast })$

Související články

• Vektorový prostor
• Vektorové pole
• Vektorový počet
• Vektorový součin
• Vektorová grafika
• Skalár
• Tenzor
• Čtyřvektor
• Diracova notace
• Souřadnicový zápis vektorů

[zobrazit] Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010
Informace o článku. Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. Tento text je dostupný za podmínek Creative Commons 3.0 Unported – creativecommons.org. Originální článek na české Wikipedii