dokončit zcela nový balíček 900 000 fotografií na plných 100 procent !!
Nedostižná hranice 4 000 000 fotografií se února 2026 už nedožije...
Kuželosečka
Z Multimediaexpo.cz
Kuželosečka je rovinná křivka, která vznikne jako průnik roviny s pláštěm rotačního kuželu (tzv. kuželová plocha), přičemž rovina neprochází jeho vrcholem.
Obsah |
Typy kuželoseček
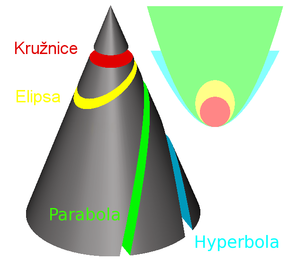
Protínáme-li kužel rovinou kolmou na osu symetrie rotačního kuželu, výslednou kuželosečkou je kružnice.
Protínáme-li kužel rovinou rovnoběžnou právě s jednou z povrchových přímek pláště kuželu, výslednou kuželosečkou je parabola.
Protínáme-li kužel rovinou, která svírá s osou symetrie rotačního kuželu úhel menší než 90° a větší než polovina vrcholového úhlu kuželu, výslednou kuželosečkou je elipsa. Rovina přitom protíná všechny povrchové přímky pláště kužele a není tedy s žádnou z nich rovnoběžná.
Protínáme-li kužel rovinou, která svírá s osou symetrie rotačního kuželu úhel menší než polovina vrcholového úhlu kuželu, výslednou kuželosečkou je hyperbola; přitom rovina je rovnoběžná právě se dvěma povrchovými přímkami kuželu.
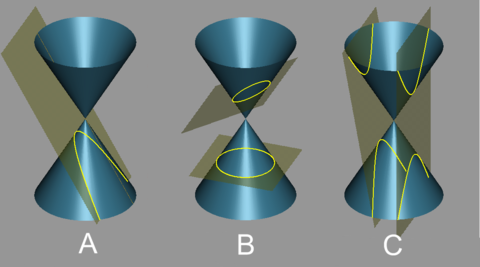
(A: parabola, B: elipsa a kružnice, C: hyperbola)
Degenerované kuželosečky
Za kuželosečku bývá často považován také průnik kuželové plochy s rovinou procházející vrcholem kuželové plochy. Takovéto kuželosečky označujeme jako degenerované (nevlastní, singulární), neboť podle polohy roviny a osy kuželové plochy dochází k redukci kuželosečky na bod, přímku nebo dvě přímky. Kuželosečky, které nejsou degenerované, tzn. kružnici, elipsu, parabolu a hyperbolu, označujeme jako vlastní (regulární) kuželosečky.
Algebraické vyjádření
Každou kuželosečku lze vyjádřit rovnicí
- \(a_{11} x^2 + 2 a_{12}xy + a_{22} y^2 + 2a_{13}x + 2a_{23}y + a_{33} = 0\),
kde koeficienty \(a_{ij}\) jsou reálná čísla, přičemž \(a_{ij}=a_{ji}\). Tato rovnice je algebraickou rovnicí druhého stupně v \(x\) a \(y\).
Invarianty
Při transformaci souřadnic se nemění některé charakteristické veličiny algebraické rovnice kuželosečky. Tyto veličiny se označují jako invarianty. Uvedená rovnice má tři invarianty:
- determinant kuželosečky
- \(\Delta = \begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{vmatrix}\)
- determinant kvadratických členů
- \(\delta = \begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix}\)
- třetím invarientem je
- \(S = a_{11} + a_{22}\)
Při transformaci souřadnic se tedy mění koeficienty \(a_{ij}\), avšak uvedené invarianty se nezmění.
Klasifikace kuželoseček podle invariantů
Invarianty rovnice kuželosečky lze použít ke klasifikaci jednotlivých křivek, které jsou touto rovnicí určeny. Je-li \(\Delta\neq 0\), pak se jedná o vlastní kuželosečku. Pro \(\Delta=0\) jde o kuželosečku degenerovanou. Rovnicemi s \(\delta=0\) jsou určeny tzv. nestředové kuželosečky (např. parabola). Pro \(\delta\neq 0\) se jedná o kuželosečky středové (např. elipsa).
| Rozdělení kuželoseček | \(\delta\neq 0\) středové kuželosečky | \(\delta=0\) nestředové kuželosečky | |||
| \(\delta>0\) | \(\delta<0\) | ||||
| \(\Delta\neq 0\) vlastní kuželosečky | \(\Delta S < 0\) reálná elipsa | hyperbola | parabola | ||
| \(\Delta S > 0\) imaginární elipsa | |||||
| \(\Delta=0\) nevlastní kuželosečky | dvojice nerovnoběžných (protínajících se) imaginárních přímek s reálným průsečíkem v nekonečnu | dvě reálné různoběžky | \(a_{13}^2 - a_{11}a_{33}<0\) dvě různé reálné rovnoběžky | \(a_{13}^2 - a_{11}a_{33} = 0\) dvě splývající rovnoběžky | \(a_{13}^2 - a_{11}a_{33} > 0\) dvě imaginární rovnoběžky |
Související články
Externí odkazy
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |