V sobotu 2. listopadu proběhla mohutná oslava naší plnoletosti !!
Multimediaexpo.cz je již 18 let na českém internetu !!

Kružnice

Z Multimediaexpo.cz

Základní atributy kružnice

V euklidovské geometrii je kružnice množina všech bodů v rovině, které leží ve stejné vzdálenosti, označované jako poloměr, od pevně daného bodu, zvaného střed. Kružnice jsou jednoduché uzavřené křivky, rozdělující rovinu na vnitřek a vnějšek. S kružnicí úzce souvisí i termín kruh, což je množina bodů složená z kružnice i jejího vnitřku, tedy všech bodů ve stejné nebo menší vzdálenosti od středu než je poloměr. Poloměrem nazýváme také každou úsečku spojující střed s bodem na kružnici. Množina všech bodů, které mají od pevného bodu \(S</math> vzdálenost nejméně \(r</math> a nejvýše \(R</math>, se nazývá mezikruží. Mezikruží je tedy část roviny nacházející se mezi dvěma kružnicemi se společným středem.

Obsah

Algebraické vyjádření

Obecná rovnice

V kartézském souřadném systému (x, y) je kružnice se středem (x0, y0) a poloměrem r množina všech bodů (x, y) vyhovujících rovnici

\(\left( x - x_0 \right)^2 + \left( y - y_0 \right)^2=r^2</math>

Pokud se střed kružnice nachází v počátku souřadnic (0, 0), lze tento vzorec zjednodušit na

\(x^2 + y^2 = r^2 \,</math>

Kružnice se středem v počátku souřadnic a poloměrem 1 se nazývá jednotková kružnice.

Vrcholová rovnice

Kružnici lze vyjádřit také tzv. vrcholovou rovnicí

\(y^2 = 2rx-x^2</math>,

která popisuje kružnici o poloměru \(r</math> se středem v bodě \([r,0]</math>.

Parametrické vyjádření

Parametrické rovnice kružnice lze zapsat jako

\(x = x_0 + r \cos\varphi</math>
\(y = y_0 + r \sin\varphi</math>

kde \(r</math> je poloměr kružnice, \([x_0,y_0]</math> je její střed a \(\varphi\in\langle 0,2\pi)</math> je proměnný parametr.

Rovnice v polárních souřadnicích

V polárních souřadnicích má rovnice kružnice o poloměru \(r</math> se středem \([\rho_0,\varphi_0]</math> tvar

\(\rho^2 - 2\rho\rho_0\cos{(\varphi-\varphi_0)}+\rho_0^2 = r^2</math>

Ve zvláštním případě, kdy střed kružnice leží na polární ose (tedy \(\varphi_0=0</math>) a počátek soustavy leží na kružnici (tedy \(\rho_0=r</math>) dostaneme rovnici

\(\rho = 2r\cos\varphi</math>

Rovnice kuželosečky

Kružnice je speciálním případem kuželosečky, konkrétně elipsy, a může být tedy vyjádřena obecnou rovnicí kuželosečky. Kružnici lze z obecné rovnice kuželosečky získat tehdy, pokud koeficienty \(a_{ij}</math> splňují podmínky

\(a_{11}=a_{22}\neq 0</math>
\(a_{12}=0</math>
\(a_{13}^2 + a_{23}^2 - a_{11} a_{33} > 0</math>

Obecnou rovnici kuželosečky lze tedy pro kružnici přepsat ve tvaru

\(a_{11}x^2+a_{11}y^2+2a_{13}x+2a_{23}y+a_{33}=0</math>

Vyjádříme-li z této rovnice poloměr kružnice, dostaneme

\(r = \frac{1}{a_{11}} \sqrt{a_{13}^2+a_{23}^2-a_{11}a_{33}}</math>

Střed této kružnice má souřadnice

\(\left[-\frac{a_{13}}{a_{11}},-\frac{a_{23}}{a_{11}}\right]</math>

Vlastnosti

Sklon (nebo derivaci) kružnice lze vyjádřit následujícím vzorcem:

\(y' = - \frac{x}{y}</math>

Všechny kružnice jsou si podobné; v důsledku toho jsou délka kružnice a její poloměr přímo úměrné, stejně jako obsah jí určeného kruhu a čtverec poloměru kružnice. Koeficienty úměrnosti činí 2π respektive π. Jinými slovy (\(r</math> je poloměr a \(d</math> průměr):

  • Délka kružnice (obvod kruhu)
\(o = 2\pi r = \pi d</math>

Délku kružnice lze odvodit pomocí pravidelného mnohoúhelníku s n vrcholy a poloměru kružnice opsané r. Mnohoúhelník je tvořen n rovnoramennými trojúhelníky. Obvod pravidelného mnohoúhelníku je dán jako n-násobek jeho strany (označíme a). Tu vypočítáme snadno pomocí funkce sinus v pravoúhlém trojúhelníku (poloviny rovnoramenného), kde přeponou je obvod opsané kružnice r, první odvěsnou poloměr vepsané kružnice v (tedy zároveň výšky rovnoramenného trojúhelníku na jeho základnu a) a druhou je polovina strany mnohoúhelníku (tj. a/2). Úhel mezi stranami r a v je polovinou hlavního vrcholu, který se dá vypočítat jako jedna n-tina plného úhlu (tj. 360° neboli 2π). Obvod se tedy rovná: \(o = 2nr \sin \frac{\pi}{n} </math> Na kružnici se můžeme dívat jako na mnohoúhelník, který má nekonečně mnoho vrcholů (úvaha viz odvození vzorce obsahu kruhu). Budeme tedy obvod kruhu počítat jako limitu obvodu mnohoúhelníku, kdy se n blíží k nekonečnu: \(o = \lim_{n \to \infty} 2nr \sin \frac{\pi}{n} = \lim_{x \to 0} \frac{2r \sin(\pi x)}{x} = 2\pi r</math>

\(S = \pi r^2 = \frac{\pi d^2}{4}</math>

Vzorec pro obsah kruhu lze odvodit ze vzorce pro jeho obvod a ze vzorce pro obsah trojúhelníku. Představme si pravidelný šestiúhelník rozdělený do stejných trojúhelníků s jejich hroty ve středu šestiúhelníku. Obsah šestiúhelníku lze zjistit pomocí vzorce pro obsah trojúhelníku sečtením délek všech základen trojúhelníků (na hranici šestiúhelníku), vynásobením jejich výškami (vzdálenost středu základny trojúhelníku do centra šestiúhelníku) a dělením dvěma. To vytvoří odhad obsahu kruhu. Představíme-li si totéž s pravidelným osmiúhelníkem, bude odhad o něco blíže obsahu kruhu. Budeme-li brát pravidelný mnohoúhelník s více a více stranami, dělit jej na trojúhelníky a počítat z nich obsah, tento obsah bude stále bližší a bližší obsahu kruhu. Blíží-li se v limitě počet stran k nekonečnu, součet jejich základen dosáhne obvodu kruhu 2πr, a výška trojúhelníků dosáhne poloměru r. Vynásobením obvodu a poloměru a vydělením 2 dosáhneme obsahu kruhu, π r². Podobně můžeme vzorec odvodit, známe-li vzorec pro výpočet obsahu pravidelného mnohoúhelníku s n vrcholy, který můžeme snadno získat s pomocí známého vzorce pro výpočet obsahu trojúhelníku: \(S=\frac{1}{2}ab\,\sin\gamma</math>, kam za a, b dosadíme poloměr opsané kružnice mnohoúhelníku a úhel γ lze vyjádřit jedna n-tina plného úhlu (tj. 360° neboli 2π). Vzorec pro obsah pravidelného mnohoúhelníku tedy vyjádříme jako: \(S = \frac{1}{2}\ n r^2 \operatorname{sin}\frac{2\pi}{n}</math> Chceme-li vypočítat obsah kruhu, stačí si představit kruh jako mnohoúhelník s nekonečným počtem vrcholů. Toto můžeme vyvodit už ze samotné definice kružnice: "Kružnice je množina všech bodů v rovině, které leží ve stejné vzdálenosti, označované jako poloměr, od pevně daného bodu, zvaného střed." Obdobně se dá zadefinovat i mnohoúhelník, který je vlastně množinou n bodů, které leží ve stejné vzdálenosti pevně daného bodu (středu). A chceme li množinu všech bodů, je jasné, že naše n bude nekonečné. Budeme tedy počítat limitu obsahu pravidelného mnohoúhelníka pro n jdoucí k nekonečnu: \(S = \lim_{n \to \infty} \frac{1}{2}\ n r^2 \operatorname{sin}\frac{2\pi}{n} = \lim_{x \to 0} \frac{r^2 \sin2\pi x}{2x} = \pi r^2</math>

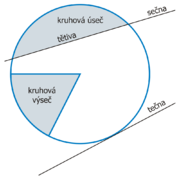
Sečna, tečna, tětiva, kruhová výseč a úseč

Sečna, tečna, tětiva, kruhová výseč a úseč

Přímka dělící kruh na dvě části se nazývá sečna a přímka dotýkající se kruhu na jednom místě se nazývá tečna. Tečny jsou vždy kolmé k spojnici bodu doteku a středu, jejíž velikost je rovna poloměru. Část sečny obklopená kružnicí se nazývá tětiva. Nejdelšími tětivami jsou ty, které prochází středem, zvané průměry, jejichž velikost je rovna dvojnásobku poloměru. Část kruhu odseknutá tětivou je kruhová úseč. Obsah kruhové úseče je dán vztahem

\(S = \frac{1}{2}[l r - t(r-v)] = \frac{r^2}{2}(\alpha-\sin\alpha)</math>,

kde \(l</math> je délka oblouku kruhové úseče, \(r</math> je poloměr kruhu, \(v</math> je výška kruhové úseče, \(t</math> je délka tětivy a \(\alpha</math> je velikost středového úhlu v obloukové míře. Část kružnice mezi dvěma poloměry se nazývá kruhový oblouk a oblast (tedy výřez kruhu) mezi poloměry a obloukem se nazývá kruhová výseč. Poměr mezi délkou oblouku a poloměrem definuje úhel mezi dvěma poloměry v radiánech. Obsah kruhové výseče lze určit ze vztahu

\(S = \frac{r^2 \alpha}{2} = \frac{l r}{2}</math>,

kde \(\alpha</math> je středový úhel v obloukové míře, \(r</math> je poloměr kruhu a \(l</math> je délka oblouku kružnice.

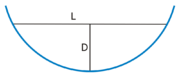
Nalezení středu z oblouku

Je-li známa pouze kružnice nebo její část, lze následujícím způsobem nalézt střed: vezměte dvě nerovnoběžné tětivy, zkonstruujte kolmice na jejich středy a zjistěte jejich průsečík. Poloměr r tohoto částečného kruhu lze spočítat z délky L tětivy a vzdálenosti D ze středu tětivy do nejbližšího bodu kružnice různými vzorce včetně:

Znázornění tětivy

(z geometrického odvození)

\(r = \frac{{\left(\frac{L}{2}\right)}^2 + D^2}{2D}</math>

(z trigonometrického odvození)

\(r = \frac{L}{\sin\left(\pi - 2 \operatorname{tg}^{-1}\frac{L}{D}\right)}</math>

Kružnice opsaná a vepsaná

Každý trojúhelník určuje několik kružnic: jeho kružnice opsaná obsahuje všechny tři vrcholy, kružnice vepsaná leží uvnitř trojúhelníku a dotýká se všech tří stran, tři kružnice připsané ležící mimo trojúhelník a dotýkající se vždy jedné strany a prodloužení zbylých dvou a kružnice devíti bodů, která obsahuje různé důležité body trojúhelníku. Thaletova věta tvrdí, že pokud tři vrcholy trojúhelníku leží na dané kružnici, v níž jedna strana trojúhelníku tvoří průměr kružnice, pak protilehlý úhel k této straně je pravý. Pro dané tři body neležící na přímce zde existuje právě jedna kružnice, která tyto body obsahuje (neboli kružnice opsaná pro trojúhelník definovaný těmito body). Pro dané tři body <(x1,y1), (x2,y2), (x3,y3)> je rovnice této kružnice dána jednoduše touto rovnicí s použitím determinantu matice: \( \det\begin{bmatrix} x & y & x^2 + y^2 & 1 \\ x_1 & y_1 & x_1^2 + y_1^2 & 1 \\ x_2 & y_2 & x_2^2 + y_2^2 & 1 \\ x_3 & y_3 & x_3^2 + y_3^2 & 1 \\ \end{bmatrix} = 0. </math> Kružnice je typem kuželosečky, kde výstřednost je rovna nule (rovina řezu je kolmá k ose kužele). V afinní geometrii se všechny kružnice a elipsy stávají (afinně) izomorfními a v projektivní geometrii se k nim ostatní kuželosečky připojují. V topologii jsou všechny jednoduché uzavřené křivky homeomorfní ke kružnicím a proto je slovo kružnice na ně často aplikováno jako na celek. Třírozměrnou analogií kruhu je koule.

Kvadratura kruhu

Kvadratura kruhu je konstrukční úloha: sestrojit k danému kruhu čtverec o stejném obsahu pouze pomocí pravítka a kružítka. Tato úloha obecně nemá řešení. Naproti tomu Tarskiho problém čtverce a kruhu je úloha rozdělit daný kruh na konečně mnoho kousků a složit z těchto kousků čtverec o stejném obsahu. S použitím axiomu výběru je tato úloha řešitelná, ovšem nikoliv prakticky. Kousky jsou neměřitelné množiny, které nelze realizovat hmotou složenou z částic. Navíc řešení, které nalezl Laczkovich, vyžaduje \(10^{50}</math> kousků. Třírozměrné tvary, jejichž průsečíky s některými rovinami dávají kruhy, jsou koule, sféroidy, válce a kužely.

Související články

Externí odkazy


Commons nabízí fotografie, obrázky a videa k tématu
Kružnice


Citováno z „http://ww2000w.multimediaexpo.cz/mmecz/index.php/Kru%C5%BEnice“