Moment hybnosti

Z Multimediaexpo.cz

Moment hybnosti je vektorová fyzikální veličina, která popisuje rotační pohyb tělesa. Moment hybnosti se určuje vzhledem k bodu nebo ose. Moment hybnosti bývá také označován jako kinetický moment, impulsmoment nebo točivost.

Obsah [skrýt] 1 Značení 2 Výpočet 2.1 Vztah k momentu síly 2.2 Vztah k plošné rychlosti 2.3 Vztah k mometu setrvačnosti 2.4 Rotační impuls 3 Vlastnosti 4 Součet momentů hybnosti vnitřních sil 5 Moment hybnosti v kvantové mechanice 6 Související články

Značení

• Symbol veličiny: $\mathbf{L}$ , někdy také b (vektor)
• Základní jednotka SI: kilogram krát metr na druhou za sekundu, značka jednotky: kg.m².s^-1

Výpočet

Moment hybnosti $\mathbf{L}$ je určen vektorovým součinem jako

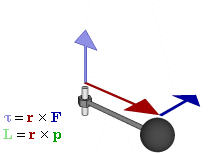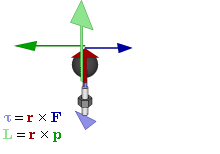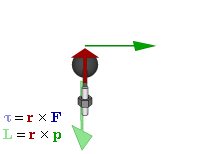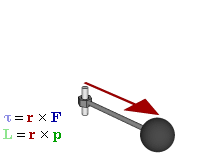
$\mathbf{L}=\mathbf{r}\times \mathbf{p}$,

kde $\mathbf{r}$ je polohový vektor a $\mathbf{p}$ je hybnost.

Vztah k momentu síly

Vyjdeme-li ze vztahu $\mathbf{M}=\mathbf{r}\times \mathbf{F}$ pro moment síly, pak lze provést následující úpravu

$\mathbf{M}=\mathbf{r}\times \mathbf{F}=\mathbf{r}\times \frac{\mathrm{d}\mathbf{p}}{\mathrm{d}t}=(\frac{\mathrm{d}\mathbf{r}}{\mathrm{d}t}\times m\mathbf{v})+(\mathbf{r}\times \frac{\mathrm{d}(m\mathbf{v})}{\mathrm{d}t})=\frac{\mathrm{d}}{\mathrm{d}t}(\mathbf{r}\times m\mathbf{v})=\frac{\mathrm{d}\mathbf{L}}{\mathrm{d}t}$,

kde $\mathbf{r}$ je polohový vektor, $\mathbf{v}=\frac{\mathrm{d}\mathbf{r}}{\mathrm{d}t}$ je rychlost, $m$ je hmotnost tělesa (hmotného bodu) pohybujícího se po kruhové dráze, $\mathbf{M}$ je moment síly a $\mathbf{L}$ je moment hybnosti, přičemž bylo využito skutečnosti, že vektorový součin $\mathbf{v}\times m\mathbf{v}$ je roven nule (tj. můžeme tento výraz k rovnici bez obav přičíst - to je ten výraz   $(\frac{\mathrm{d}\mathbf{r}}{\mathrm{d}t}\times m\mathbf{v})$). Předchozí vztah lze slovně popsat tak, že změna momentu hybnosti vzhledem k pevnému bodu $O$ je co do velikosti i směru rovna momentu síly (vzhledem k témuž bodu), který na hmotný bod působí. V soustavě hmotných bodů platí pro $i$-tý hmotný bod podle vztah ${\mathbf{M}}_i=\frac{\mathrm{d}{\mathbf{L}}_i}{\mathrm{d}t}$. Z vlastností momentu síly pak plyne

$\mathbf{M}=\sum _{i=1}^n{\mathbf{M}}_i=\sum _{i=1}^n\frac{\mathrm{d}{\mathbf{L}}_i}{\mathrm{d}t}=\frac{\mathrm{d}}{\mathrm{d}t}\sum _{i=1}^n{\mathbf{L}}_i=\frac{\mathrm{d}\mathbf{L}}{\mathrm{d}t}$,

kde $\mathbf{L}=\sum _{i=1}^n{\mathbf{L}}_i$ představuje celkový moment hybnosti.

Vztah k plošné rychlosti

S využitím druhého Keplerova zákona lze vyjádřit vztah mezi plošnou rychlostí $\mathbf{w}$ a momentem hybnosti jako

$\mathbf{L}=2m\mathbf{w}$

Vztah k mometu setrvačnosti

Při kruhovém pohybu lze rychlost vyjádřit jako $\mathbf{v}=\omega \times \mathbf{r}$. Moment hybnosti soustavy $n$ hmotných bodů vzhledem k těžišti lze pak vyjádřit vztahem

$\mathbf{L}=\sum _{i=1}^n[{\mathbf{r}}_i\times m_i(\omega \times {\mathbf{r}}_i)]$

kde ${\mathbf{r}}_i$ označuje polohu $i$-tého hmotného bodu s hmotností $m_i$ vzhledem k těžišti a $\omega$ je úhlová rychlost pohybu tělesa kolem osy rotace jdoucí těžištěm. Použitím dvojitého vektorového součinu dostaneme

$\mathbf{L}=\sum _{i=1}^n{m}_i[r_i^2\omega -(\omega \cdot {\mathbf{r}}_i){\mathbf{r}}_i]$

Točivost tělesa vzhledem k těžišti má tedy dvě složky. První má směr úhlové rychlosti, tedy směr osy rotace, druhá má ale jiný směr. Točivost tedy obecně nemá směr rotační osy. Označíme-li složky úhlové rychlosti $\omega$ vhledem k libovolné soustavě souřadnic s počátkem v těžišti a pevně spojené s tělesem jako ${\omega }_x,{\omega }_y,{\omega }_z$ a složky průvodiče ${\mathbf{r}}_i$ jako $x_i,y_i,z_i$, můžeme předchozí vztah rozepsat do složek. Z vajádření momentu setrvačnosti $J$ pak lze získat

$L_x={\omega }_x{J}_x-{\omega }_y{D}_{xy}-{\omega }_z{D}_{zx}$

$L_y={\omega }_y{J}_y-{\omega }_z{D}_{yz}-{\omega }_x{D}_{xy}$

$L_z={\omega }_z{J}_z-{\omega }_x{D}_{zx}-{\omega }_y{D}_{yz}$

kde $J_i$ jsou momenty setrvačnosti k $i$-té ose a $D_{ij}$ jsou deviační momenty. Pokud vztáhneme složky točivosti k soustavě souřadnic totožné s hlavními osami centrálního elipsoidu setrvačnosti, deviační momenty vymizí, a složky točivosti vzhledem k hlavním osám budou

$L_1=J_1{\omega }_1$

$L_2=J_2{\omega }_2$

$L_3=J_3{\omega }_3$

Pokud se těleso otáčí kolem osy, která je totožná s jednou z hlavních os setrvačnosti nebo kolem pevné osy, jsou složky úhlové rychlosti k osám kolmým k rotační ose nulové a točivost lze zapsat jako

$\mathbf{L}=J\omega$

Rotační impuls

Pro časový účinek momentu síly můžeme v analogii s impulsem síly získat vztah pro rotační impuls $\mathbf{b}$

$\mathbf{L}-{\mathbf{L}}_0={\int }_{t_0}^t\mathbf{M}\mathrm{d}t=\mathbf{b}$

Pokud je silový moment $\mathbf{M}$ po celou dobu působení stálý, je možné předchozí výraz zjednodušit na tvar

$\mathbf{L}-{\mathbf{L}}_0=\mathbf{M}(t-t_0)$

Vlastnosti

Moment hybnosti má při rotačním pohybu stejný význam jako hybnost při pohybu přímočarém. Pojem momentu hybnosti je analogický pojmu hybnosti: tak jako je hybnost součinem hmotnosti a rychlosti v případě translačního pohybu, tak je moment hybnosti součinem momentu setrvačnosti a úhlové rychlosti v případě rotačního pohybu.

Součet momentů hybnosti vnitřních sil

Součet momentů hybnosti vnitřních sil v tuhém tělese je roven nule, protože: 1. Dva body na sebe působí silou přitažlivou nebo odpudivou (tzn. má směr shodný se směrem jejich spojnice) 2. Působí-li bod A na bod B, pak bod B působí na bod A silou stejně velikou, ale opačně orientovanou Uvažme tedy vzoreček pro moment sil: ${\mathbf{M}}_i$ je moment hybnosti $i$-tého bodu. Mezi $i$-tým a $j$-tým bodem působí síla ${\mathbf{F}}_{i,j}=-{\mathbf{F}}_{j,i}$. Celkový moment hybnosti vnitřních sil je $\sum {\mathbf{M}}_i=\sum _i{\mathbf{r}}_i\times \sum _j{\mathbf{F}}_{i,j}=\sum _i\sum _j{\mathbf{r}}_i\times {\mathbf{F}}_{i,j}$. Uvažujme nyní pouze interakci $i$-tého a $j$-tého bodu: ${\mathbf{r}}_i\times {\mathbf{F}}_{i,j}+{\mathbf{r}}_j\times {\mathbf{F}}_{j,i}={\mathbf{r}}_i\times {\mathbf{F}}_{i,j}-{\mathbf{r}}_j\times {\mathbf{F}}_{i,j}=({\mathbf{r}}_i-{\mathbf{r}}_j)\times {\mathbf{F}}_{i,j}$, kde ${\mathbf{r}}_i-{\mathbf{r}}_j$ je spojnice $i$-tého a $j$-tého bodu. Dle prvního předpokladu na sebe tyto body působí silou, která je s jejich spojnicí rovnoběžná. A jak známo, vektorový součin rovnoběžných vektorů je roven nule.

Moment hybnosti v kvantové mechanice

V kvantové mechanice je moment hybnosti vždy kvantován. Výsledkem měření jedné komponenty momentu hybnosti (impulsmomentu) můžou být pouze násobky redukované Planckovy konstanty. Kvantován je i kvadrát momentu hybnosti. Zcela novou vlastností je spin částic, vnitřní moment hybnosti určité částice. Na rozdíl od orbitálního impulsmomentu, který byl zmíněn výše může nabývat komponenta spinu i poločíselných hodnot. Při zavedení kvantového impulsmomentu vyjdeme z principu korespondence, kvantový impulsmoment je tedy definován takto: $\hat{\mathbf{L}}=\hat{\mathbf{r}}\times \hat{p}$ Z komutačních relací pro souřadnici a impuls $[{\hat{X}}_k,{\hat{P}}_l]=i\hslash {\delta }_{kl}$ lze odvodit komutační relace pro impulsmoment: $[{\hat{L}}_k,{\hat{L}}_l]=i\hslash {\epsilon }_{kln}{\hat{L}}_n$ Z těchto komutačních relací již plyne kvantování impulsmomentu. Pro vlastní vektory kvadrátu impulsmomentu a jeho třetí komponenty platí: ${\hat{\mathbf{L}}}^{\mathbf{2}}|lm⟩={\hslash }^{2}l(l+1)|lm⟩$ ${\hat{L}}_3|lm⟩=\hslash m|lm⟩$ Kde l je nezáporné celé nebo polocelé číslo. Pro určitou hodnotu l může kvantové číslo m nabývat pouze hodnot -l,-l+1,...,l-1,l, tedy celkem 2l+1 hodnot.

Související články

• Hybnost
• Moment setrvačnosti
• Zákon zachování momentu hybnosti
• Rotační pohyb

[zobrazit] Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010
Informace o článku. Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. Tento text je dostupný za podmínek Creative Commons 3.0 Unported – creativecommons.org. Originální článek na české Wikipedii