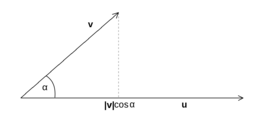The final launch of the Allmultimedia.org will take place on February 24, 2026
(shortly after the 2026 Winter Olympics).
Skalární součin
Z Multimediaexpo.cz
Skalární součin je v matematice zobrazení, které dvojici vektorů přiřadí číslo (skalár), které má vztah k velikosti těchto vektorů, k tzv. ortogonalitě a případně k úhlu, který svírají.
Formálně se skalární součin definuje na reálném nebo komplexním vektorovém prostoru V jako bilineární zobrazení
- \(V\times V \to \mathbb{R}\) resp. \(V\times V \to \mathbb{C}\), kde \(V\) je vektorový prostor nad číselným tělesem \(\mathbb{R}\) resp. \(\mathbb{C}\),
splňující jisté vlastnosti.
Nejběžnější příklad skalárního součinu je v trojrozměrném eukleidovském prostoru zobrazení dané vzorcem
- \(\mathbf{a}\cdot\mathbf{b} = a_1 b_1 + a_2 b_2 + a_3 b_3 = |\mathbf{a}|\,|\mathbf{b}| \cos \alpha\),
kde \(\alpha\) je úhel sevřený vektory a a b.
Obsah |
Způsob zápisu
Nejběžnější způsoby zápisu skalárního součinu vektorů u, v jsou:
- \(\mathbf{u} \cdot \mathbf{v}\) – značení používané hlavně v prostorech konečné dimenze. Jedná se o podobné značení jako u násobení matic, což je v určitých ohledech podobná operace.
- \(\langle \mathbf{u},\mathbf{v} \rangle\) – značení běžné ve funkcionální analýze.
- \((\mathbf{u},\mathbf{v})\) – starší značení, dnes již méně používané.
- \(b\,(\mathbf{u},\mathbf{v})\) – b jako bilineární forma
- \(\langle \mathbf{v} \mid \mathbf{u} \rangle\) – při použití Diracovy notace v kvantové mechanice
Definice
Jsou dány číselné těleso T a vektorový prostor V nad tímto tělesem. Zobrazení V×V → T je skalárním součinem, jestliže splňuje pro všechna \(\mathbf{u}, \mathbf{v}, \mathbf{w} \in V\) a všechna \(a \in T\) následující podmínky:
- \((\mathbf{u},\mathbf{v}) = \overline{(\mathbf{v},\mathbf{u})}\)
- \((\mathbf{u}+\mathbf{v},\mathbf{w}) = (\mathbf{u},\mathbf{w})+(\mathbf{v},\mathbf{w})\)
- \((a\,\mathbf{u},\mathbf{v}) = a\,(\mathbf{u},\mathbf{v})\)
- \((\mathbf{v},\mathbf{v}) \ge 0\)
- \((\mathbf{v},\mathbf{v}) = 0 \iff \mathbf{v} = \mathbf{0}\)
Pruhem je označeno komplexní sdružení. Pro reálná čísla platí \(\overline x = x.\)
Vlastnosti
- v reálném vektorovém prostoru je skalární součin komutativní, tzn.
- \((\mathbf{u},\mathbf{v}) = (\mathbf{v},\mathbf{u})\)
- ve vektorovém prostoru nad tělesem komplexních čísel platí
- \((\mathbf{u},\mathbf{v}) = \overline{(\mathbf{v},\mathbf{u})}\)
- pro komplexní a platí
- \((\mathbf{u},a\,\mathbf{v}) = \overline{a}\,(\mathbf{u},\mathbf{v})\)
- vektory u, v nazýváme ortogonálními vektory, pokud splňují vztah
- \((\mathbf{u},\mathbf{v}) = 0\)
- jestliže množina \(\{\mathbf{e}_1,\mathbf{e}_2,\dots,\mathbf{e}_n\}\) vyhovuje vztahu
- \((\mathbf{e}_j,\mathbf{e}_k) = \delta_{jk}\), kde \(\delta_{jk}\) je Kroneckerovo delta,
- pak tyto vektory označujeme jako ortonormální.
- pomocí skalárního součinu lze definovat normu vektoru, tzv.
- norma generovaná skalárním součinem:
- \(\|\mathbf{v}\| = \sqrt{(\mathbf{v},\mathbf{v})}\)
- z geometrického hlediska představuje skalární součin vektorů u, v součin velikosti vektoru u a velikosti průmětu v do směru vektoru u, tzn.
- \(\mathbf{u}\cdot \mathbf{v} = \|\mathbf{u}\|\,\|\mathbf{v}\| \cos \alpha\),
- kde \(\alpha\) je úhel, který svírají vektory u, v.
Příklady skalárních součinů
- pro dva vektory \(\mathbf{u}=\sum_{i=1}^n u^i \mathbf{e}_i,\, \mathbf{v}=\sum_{i=1}^n v^i \mathbf{e}_i\)
- (zapsané v nějaké jedné pevně zvolené bázi \(\mathbf{e}\)) lze skalární součin definovat jako
- \((\mathbf{u}, \mathbf{v}) = \sum^n_{i,j=1} (\mathbf{e}_i,\mathbf{e}_j) u^i \overline{v^j} = \sum^n_{i,j=1} g_{i j}u^i \overline{v^j}\),
- kde \(g_{i j} = (\mathbf{e}_i,\mathbf{e}_j)\) je metrický tenzor (v tomto případě matice).
- pro dvě posloupnosti \(a,b : \mathbb{N} \to \mathbb{C}\) můžeme definovat skalární součin jako řadu
- \((a, b) = \sum_{i=0}^{\infty} a_i \overline{b_i}\)
- pokud řada konverguje.
- skalární součin funkcí \((f, g)=\int_a^b f(x)\cdot \overline{g(x)} dx\) pokud integrál konverguje. (meze integrace jsou obvykle \(0, \pm \infty, \pm 1, \pm \pi\))
Příklad výpočtu skalárního součinu
Mějme dva trojrozměrné vektory a = (1,2,3), b = (4,5,6). Potom jejich skalární součin je
- \(\mathbf{a} \cdot \mathbf{b} = a_ 1b_1 + a_2 b_2 + a_3 b_3 = 1\cdot 4 + 2\cdot 5 + 3\cdot 6 = 32\).
Související články
Externí odkazy
|
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |