V sobotu 2. listopadu proběhla mohutná oslava naší plnoletosti !!
Multimediaexpo.cz je již 18 let na českém internetu !!
V tiskové zprávě k 18. narozeninám brzy najdete nové a zásadní informace.

Heronův vzorec

Z Multimediaexpo.cz

(Rozdíly mezi verzemi)
(+ Nový článek)
(+ Aktualizace)
 
(Není zobrazena jedna mezilehlá verze.)
Řádka 1: Řádka 1:
-
{{Wikipedia-cs|Heronův vzorec|700}}
+
'''Heronův vzorec''' je [[vzorec]] pro výpočet [[obsah]]u obecného [[trojúhelník]]u (v euklidovské rovině) pomocí délek jeho stran.
 +
== Vzorec ==
 +
Jsou-li <big>\(a, b, c\)</big> délky stran trojúhelníka, platí pro jeho obsah
 +
:<big>\( S = \sqrt{ s(s-a)(s-b)(s-c)},\)</big>
 +
kde <big>\( s= \frac {a + b +c}{2}\)</big> je poloviční [[Obvod (geometrie)|obvod]] trojúhelníku.
 +
 +
== Důkaz ==
 +
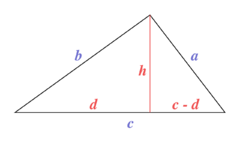
[[Soubor:Triangle with notations 3.png|thumb|240px]]
 +
Označme ''x'' vzdálenost vrcholu B od paty kolmice z vrcholu A na stranu a (výšky). Pro pravoúhlý trojúhelník na obrázku platí:
 +
 +
<big>\( \ x^2 + v^2 = c^2 \)</big><br /><br />
 +
<big>\( \ (a-x)^2 + v^2 = b^2 \)</big><br /><br />
 +
Odečteme-li od druhé rovnice první, dostaneme:
 +
 +
<big>\( \ a^2 - 2ax = b^2 - c^2 \)</big><br /><br />
 +
Z tohoto vztahu vyjádříme x:<br /><br />
 +
<big>\( x= \frac {a^2 + c^2 - b^2}{2a} \)</big><br /><br />
 +
Toto platí i v pravoúhlém trojúhelníku, v tupoúhlém s opačným znaménkem. Jestliže za x dosadíme do první rovnice, získáme výšku v:
 +
 +
<big>\( \ v^2 = c^2 - x^2 \)</big><br /><br />
 +
<big>\( v^2 = c^2 - \left(\frac {a^2 + c^2 - b^2}{2a}\right)^2 \)</big><br / ><br />
 +
<big>\( v^2 = c^2 - \frac {\left(a^2 + c^2 - b^2\right)^2}{4a^2} \)</big><br /><br />
 +
<big>\( v^2 =\frac{4c^2a^2 - \left(a^2 + c^2 - b^2\right)^2}{4a^2} \)</big><br /><br />
 +
<big>\( v =\frac{\sqrt{4c^2a^2 - \left(a^2 + c^2 - b^2\right)^2}}{2a} \)</big><br /><br />
 +
Dosadíme-li tuto výšku do vzorce pro obsah trojúhelníku
 +
 +
<big>\( S= \frac {av}{2}, \)</big><br /><br />
 +
dostaneme
 +
 +
<big>\( S= \frac {\sqrt{4c^2a^2 - \left(a^2 + c^2 - b^2\right)^2}}{4} \)</big><br /><br />
 +
Dále pomocí rozkladů upravíme výraz pod odmocninou:
 +
 +
<big>\( S= \frac {\sqrt{\left(2ac + a^2 + c^2 - b^2\right)\left(2ac - a^2 - c^2 + b^2\right)}}{4} \)</big><br /><br />
 +
<big>\( S= \frac {\sqrt{\left[\left(a + c \right)^2 - b^2\right]\left[b^2 - \left(a - c \right)^2\right]}}{4} \)</big><br /><br />
 +
<big>\( S= \frac {\sqrt{\left(a + c + b\right)\left(a + c - b\right)\left(b + a - c\right)\left(b - a + c\right)}}{4} \)</big><br /><br />
 +
Dosadíme poloviční obvod s,
 +
 +
<big>\( \ a + b + c = 2s  \)</big><br /><br />
 +
a dostáváme výsledný vzorec:
 +
 +
<big>\( S= \frac {\sqrt{2s\left(2s - 2a\right)\left(2s - 2b\right)\left(2s - 2c\right)}}{4} \)</big><br /><br />
 +
<big>\( S= \frac {\sqrt{16s\left(s - a\right)\left(s - b\right)\left(s - c\right)}}{4} \)</big><br /><br />
 +
<big>\( S= \sqrt{s\left(s - a\right)\left(s - b\right)\left(s - c\right)} \)</big><br /><br />
 +
 +
== Historie ==
 +
Vzorec byl formulován Hérónem z Alexandrie a důkaz byl publikován v jeho knize [[Métrika]], napsané v první polovině 1. století.<ref>http://mathworld.wolfram.com/HeronsFormula.html</ref>
 +
 +
== Poznámky ==
 +
Kratší důkaz je možný pomocí [[kosinová věta|kosinové věty]].
 +
 +
Heronův vzorec je limitním případem [[Brahmaguptův vzorec|Brahmaguptova vzorce]] pro obsah [[tětivový čtyřúhelník|tětivového čtyřúhelníku]].
 +
 +
Obsah trojúhelníku je symetrická kvadraticky homogenní funkce jeho stran, H. v. ukazuje její konkrétní tvar.
 +
 +
== Související články ==
 +
* [[Trojúhelník]]
 +
* [[Obsah]]
 +
* [[Tětivový čtyřúhelník]]
 +
== Reference ==
 +
<references />
 +
== Externí odkazy ==
 +
* [https://web.archive.org/web/20070526232505/http://www.zshorakhk.cz/matematika/ulohy/heron/dheron.html Důkaz heronova vzorce]
 +
 +
 +
{{Commonscat|Heron's formula}}{{Článek z Wikipedie}}
[[Kategorie:Matematické věty a důkazy]]
[[Kategorie:Matematické věty a důkazy]]
[[Kategorie:Trojúhelník]]
[[Kategorie:Trojúhelník]]

Aktuální verze z 22. 8. 2022, 12:51

Heronův vzorec je vzorec pro výpočet obsahu obecného trojúhelníku (v euklidovské rovině) pomocí délek jeho stran.

Obsah

Vzorec

Jsou-li \(a, b, c\) délky stran trojúhelníka, platí pro jeho obsah

\( S = \sqrt{ s(s-a)(s-b)(s-c)},\)

kde \( s= \frac {a + b +c}{2}\) je poloviční obvod trojúhelníku.

Důkaz

Triangle with notations 3.png

Označme x vzdálenost vrcholu B od paty kolmice z vrcholu A na stranu a (výšky). Pro pravoúhlý trojúhelník na obrázku platí:

\( \ x^2 + v^2 = c^2 \)

\( \ (a-x)^2 + v^2 = b^2 \)

Odečteme-li od druhé rovnice první, dostaneme:

\( \ a^2 - 2ax = b^2 - c^2 \)

Z tohoto vztahu vyjádříme x:

\( x= \frac {a^2 + c^2 - b^2}{2a} \)

Toto platí i v pravoúhlém trojúhelníku, v tupoúhlém s opačným znaménkem. Jestliže za x dosadíme do první rovnice, získáme výšku v:

\( \ v^2 = c^2 - x^2 \)

\( v^2 = c^2 - \left(\frac {a^2 + c^2 - b^2}{2a}\right)^2 \)

\( v^2 = c^2 - \frac {\left(a^2 + c^2 - b^2\right)^2}{4a^2} \)

\( v^2 =\frac{4c^2a^2 - \left(a^2 + c^2 - b^2\right)^2}{4a^2} \)

\( v =\frac{\sqrt{4c^2a^2 - \left(a^2 + c^2 - b^2\right)^2}}{2a} \)

Dosadíme-li tuto výšku do vzorce pro obsah trojúhelníku

\( S= \frac {av}{2}, \)

dostaneme

\( S= \frac {\sqrt{4c^2a^2 - \left(a^2 + c^2 - b^2\right)^2}}{4} \)

Dále pomocí rozkladů upravíme výraz pod odmocninou:

\( S= \frac {\sqrt{\left(2ac + a^2 + c^2 - b^2\right)\left(2ac - a^2 - c^2 + b^2\right)}}{4} \)

\( S= \frac {\sqrt{\left[\left(a + c \right)^2 - b^2\right]\left[b^2 - \left(a - c \right)^2\right]}}{4} \)

\( S= \frac {\sqrt{\left(a + c + b\right)\left(a + c - b\right)\left(b + a - c\right)\left(b - a + c\right)}}{4} \)

Dosadíme poloviční obvod s,

\( \ a + b + c = 2s \)

a dostáváme výsledný vzorec:

\( S= \frac {\sqrt{2s\left(2s - 2a\right)\left(2s - 2b\right)\left(2s - 2c\right)}}{4} \)

\( S= \frac {\sqrt{16s\left(s - a\right)\left(s - b\right)\left(s - c\right)}}{4} \)

\( S= \sqrt{s\left(s - a\right)\left(s - b\right)\left(s - c\right)} \)

Historie

Vzorec byl formulován Hérónem z Alexandrie a důkaz byl publikován v jeho knize Métrika, napsané v první polovině 1. století.[1]

Poznámky

Kratší důkaz je možný pomocí kosinové věty.

Heronův vzorec je limitním případem Brahmaguptova vzorce pro obsah tětivového čtyřúhelníku.

Obsah trojúhelníku je symetrická kvadraticky homogenní funkce jeho stran, H. v. ukazuje její konkrétní tvar.

Související články

Reference

  1. ↑ http://mathworld.wolfram.com/HeronsFormula.html

Externí odkazy


Commons nabízí fotografie, obrázky a videa k tématu
Heronův vzorec
Citováno z „http://ww2000w.multimediaexpo.cz/mmecz/index.php/Heron%C5%AFv_vzorec“