Návštěvnost dne 25. února 2026 byla — 484 927 unikátních návštěvníků !
Návštěvnost dne 26. února 2026 byla — 479 665 unikátních návštěvníků !
Návštěvnost dne 5. března 2026 byla — 475 445 unikátních návštěvníků !
Pružnost
Z Multimediaexpo.cz
Pružnost (též elasticita či tuhost) je část mechaniky, která studuje vztahy mezi deformacemi těles a vnějšími silami, které na toto těleso působí. V úlohách pružnosti se potom řeší, zda deformace tělesa či konstrukce nepřesáhla dovolenou hodnotu.[1]
Jedním z prvních, kdo se zabýval hledáním vztahů mezi silami působícími na těleso a deformacemi tělesa způsobenými těmito silami, byl britský fyzik Robert Hooke. Hooke v roce 1676 zformuloval zákon, jenž říká, že při pružné deformaci je normálové napětí přímo úměrné relativnímu prodloužení.[2] Tento poznatek je v podstatě jedním ze základních kamenů matematické teorie pružnosti a v nezměněné podobě se využívá dodnes. Zákon, který Hooke definoval, nese jeho jméno.
Obsah |
Rozdělení, základní pojmy a předpoklady
Rozdělení pružnosti
Pružnost lze velmi obecně rozdělit na několik vzájemně souvisejících oddílů.
- Matematická teorie pružnosti využívá nejméně zjednodušujících předpokladů a snaží se nalézt analytická (tedy obecná a přesná) řešení úloh a problémů.
- Experimentální pružnost se používá pro ověření složitých výpočtů a pro stanovení materiálových charakteristik jako je modul pružnosti v tahu, modul pružnosti ve smyku apod.
- Mechanika kompozitních materiálů zkoumá chování kompozitních materiálů, přičemž využívá jak poznatky pružnosti, tak poznatky pevnosti.
Základní předpoklady
Poznatky z pružnosti lze využít jen při splnění několika předpokladů. Praxe ukazuje, že teoretické vztahy lze využít, i když se vlastnosti reálného tělesa či konstrukce prvním dvěma předpokladům pouze blíží.
- Těleso uvažujeme jako homogenní, tj. těleso má stejné mechanické vlastnosti v každém bodě.
- Těleso uvažujeme jako izotropní, tj. těleso má stejné mechanické vlastnosti ve všech směrech.
- Deformace tělesa je malá a pružná, což jinými slovy znamená, že se tato deformace pohybuje v oblasti platnosti Hookeova zákona a těleso se po odlehčení vrátí do svého původního tvaru.
Základní pojmy
Pružné těleso
Pružné těleso (též elastické těleso) je takové těleso, které se působením vnější síly deformuje, ale po odstranění této síly se vrací do původního tvaru. Tělesa, která se po odstranění vnější síly nevrátí do původního tvaru, se označují jako nepružná (též plastická tělesa).
Vnější síla
Pojmem vnější síla lze v pružnosti označit veškeré síly působící na těleso (nebo konstrukci), které mají původ mimo těleso. Tato definice však není úplně přesná, neboť mezi vnější síly počítáme i tíhovou sílu způsobenou vlastní hmotností tělesa.
Podle oblasti působení rozlišujeme vnější síly povrchové a objemové.
Povrchové vnější síly působící na povrch tělesa mohou být osamělé, ty potom působí na povrch v jediném bodě, nebo spojité, které spojitě působí na určitou část povrchu.
Objemovou vnější sílou rozumíme vlastní tíhu tělesa či konstrukce (která spojitě vychází z vlastního objemu tělesa).
Z hlediska času můžeme těleso či konstrukci zatížit staticky, kdy jsou vnější síly konstantní v čase, nebo se velmi pomalu mění, cyklicky, kdy se vnější síly mění v čase periodicky, či rázově, kdy (obvykle velmi velká síla) působí na těleso po velmi malý časový interval (obvykle se jedná o mikrosekundy až milisekundy).
Vnitřní síla
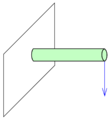
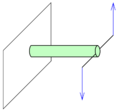
Vlivem působení vnějších sil se těleso deformuje a rovněž v něm vzniknou tzv. vnitřní síly, které odporují vnějším silám. Velikost a směr vnitřních sil se určuje metodou řezu. Vnitřní síla se v každém řezu rozkládá do dvou složek a to do normálové, která je kolmá na rovinu řezu, a do tečné, která leží v rovině řezu.
Napětí a deformace
Napětí a deformace vyjadřují intenzitu vnitřních sil.
Napětí
Napětí se vztahuje k danému řezu v tělese, jeho jednotkou je pascal, případně newton na metr čtvereční. Protože rozlišujeme dvě složky vnitřní síly, normálovou a tečnou, budeme rozlišovat i dvě složky napětí, normálové napětí a smykové (tečné) napětí.
Normálové napětí tedy vypočteme jako podíl normálově složky vnitřní síly a obsahu plochy řezu
- \(\sigma = \frac{F_n}{S} = \frac{N}{A}\).
Přejdeme-li k diferenciálně malé plošce řezu, platí vztah
- \(\sigma = \frac{\mathrm{d}N}{\mathrm{d}A}\).
Smykovou složku napětí lze obdobně vyjádřit jako podíl tečné složky vnitřní síly a obsahu plochy příslušného řezu
- \(\tau = \frac{F_t}{S} = \frac{T}{A}\).
Pro diferencíálně malou plošku řezu opět platí
- \(\tau = \frac{\mathrm{d}T}{\mathrm{d}A}\).
V technické praxi se obvykle normálová složka síly značí písmenem \(N\), tečná \(T\) a plocha řezu \(A\).
Deformace
Oproti napětí se deformace (těž prodloužení, přetvoření nebo zkrácení) vztahuje k danému rozměru tělesa. Jde ale o bezrozměrnou veličinu, neboť udává poměr mezi prodloužením (zkrácením) a původním rozměrem. Protože se pohybujeme v oblasti malých deformací, je možno vztah pro výpočet poměrného prodloužení \(\varepsilon\) zjednodušit, jak je naznačeno dále, bez (velké) újmy na přesnosti
- \(\varepsilon = \frac{\Delta l}{\Delta l + l_0} \approx \frac{\Delta l}{l_0}\).
Výše uvedený vzorec udává prodloužení tělesa způsobené normálovou složkou vnitřní síly. Je zřejmé, že i tečná složka vnitřní síly způsobuje nějakou deformaci a tou je natočení roviny řezu, tzv. skos \(\gamma\) vyjadřující poměr mezi výškou řezu \(h\) a vzdáleností mezi původní polohou krajního bodu řezu a novou polohou krajního bodu řezu \(a\). Vztah pro výpočet skosu jde opět díky základním předpokladům pružnosti zjednodušit
- \(\tan \gamma \approx \gamma = \frac{a}{h}\),
neboť za předpokladu, že úhel \(\alpha\) je menší než 5° (což je splněno, neboť předpokládáme malé deformace) platí přibližná rovnost
- \(\tan \alpha\approx \alpha\).
Vztah mezi napětím a deformací
Vztah mezi napětím a deformací vyjadřuje Hookeův zákon, omezíme-li se tedy na oblast platnosti tohoto zákona, pro tah (resp. tlak) platí
- \(\sigma = E \cdot \varepsilon\),
kde \(E\) je modul pružnosti v tahu (též Youngův modul pružnosti).[1] Podobně pro skos můžeme definovat vztah, někdy nazývaný Hookeův zákon pro smyk,
- \(\tau = G \cdot \gamma\),
kde \(G\) je modul pružnosti ve smyku.
Srovnáme-li všechny uvedené vztahy, můžeme v případě, kdy je součást konstantního průřezu \(A\) namáhána jenom normálovou silou \(N\), určit prodloužení na základě znalostí počátečních podmínek ze vztahu
- \(\Delta l = \varepsilon \cdot l_0 = \frac {\sigma}{E} \cdot l_0 = \frac {N \cdot l_0}{E \cdot A}= \frac {F \cdot l_0}{E \cdot A}\)
kde \(\Delta l\) je absolutní změna délky součásti a \(l_0\) její původní délka.[1]
Tahový a pracovní diagram
Přesnější vztah mezi napětím a deformací lze získat experimentálně, provedením tahové zkoušky, kdy nejsme omezeni oblastí platnosti Hookeova zákona.
Po provedení tahové zkoušky je možno vytvořit tahový diagram, zobrazující závislost mezi silou \(F\), kterou působíme na vzorek (obvykle tyč normované délky a normovaného průřezu) a délkou \(\Delta l\), o níž se sledovaný vzorek prodlouží. Matematicky lze tento vztah zapsat \(F = F (\Delta l)\).
Často se zavádí pracovní diagram, vyjadřující závislost napětí na deformaci, matematicky \(\sigma = \sigma (\varepsilon)\). Myšlenka přechodu od tahového diagramu k pracovnímu je velmi jednoduchá: uvědomíme-li si, že pro napětí platí vztah \(\sigma = F / A_0\) a deformaci je možno určit jako \(\varepsilon = \Delta l / l_0\), přičemž \(A_0\) i \(l_0\) jsou pro měřený vzorek konstanty (jak už bylo zmíněno výše, jde o obsah průřezu a délku nenamáhaného vzorku), můžeme pomocí známých vzorců spočítat napětí \(\sigma\) a deformaci \(\varepsilon\).
Je třeba si uvědomit důležitou skutečnost: je-li vzorek natahován, jeho průřez \(A\) se zmenšuje. V naší úvaze však napětí \(\sigma\) počítáme díky znalosti obsahu průřezu nenamáhaného vzorku \(A_0\). Tento však obecně není konstantní a proto se skutečné napětí může i značně lišit od napětí námi spočítaného. Z tohoto důvodu se zavádí pojmy smluvní pracovní diagram a skutečný pracovní diagram. Oba diagramy znázorňují závislost napětí na deformaci, ve smluvním pracovním diagramu však napětí vztahujeme ke klidovému průřezu \(A_0\), zatímco ve skutečném pracovním diagramu napětí vztahujeme ke skutečnému průřezu. Je tedy zjevné, že ve smluvním diagramu je sice napětí zdánlivé, ale jeho vytvoření je snazší, zatímco ve skutečném diagramu je skutečné napětí, ale vzhledem k proměnnému průřezu je jeho vytvoření složitější.
Na základě podobnosti pracovních (či tahových) diagramů lze jednotlivé materiály rozdělit do několika skupin, o nichž bude řeč dále.
Zbývá dodat, že křivky v tahovém i smluvním pracovním diagramu mají pro daný materiál stejný průběh.
Houževnatý materiál
Houževnaté materiály se vyznačují stejným chováním v tahu i tlaku a obvykle i vysokou pevností. Mezi houževnaté materiály patří například houževnatá ocel.
Dále je pomocí pracovního diagramu popsáno chování houževnatého materiálu, respektive závislost napětí na jeho deformaci.
Hodnota \(\sigma_u\) v diagramu se nazývá mez úměrnosti. V intervalu od nulového napětí do meze úměrnosti platí Hookeův zákon a veškeré deformace jsou elastické (bývají značeny \(\varepsilon_e\)), což znamená, že po odstranění zatížení deformace zmizí a délka namáhané součásti se vrátí na původní délku \(l_0\).
Hodnota \(\sigma_E\) označuje mez pružnosti, zvanou též mez elasticity. Mez pružnosti se obvykle příliš neliší od meze úměrnosti. Při zvýšení napětí nad mez pružnosti dochází po odstranění zatížení k tomu, že deformace nezmizí úplně, ale zůstává jistá trvalá (tzv. plastická) deformace (značí se \(\varepsilon_p\)).
Napětím \(\sigma_k\) (v novější literatuře \(R_e\)) je určena mez kluzu nebo mez průtažnosti. Součást se v tomto bodě prodlužuje, aniž by se zvětšovalo zatížení. Rovněž dochází ke změně fyzikálních vlastností materiálu, kdy krystalové mřížkou kloužou po sobě (proto mez kluzu) a v důsledku jeho přetvoření také k mírnému zpevnění.
U některých materiálů jsou hodnoty \(\sigma_u\), \(\sigma_e\) a \(\sigma_n\) prakticky totožné. O takových materiálech říkáme, že nemají výraznou mez skluzu a zavádíme tzv. smluvní mez skluzu \(R_{p02}\), což je hodnota napětí způsobující plastickou deformaci 0,2%.[3]
Při dalším zvyšování zatížení dosáhneme meze pevnosti \(\sigma_p\) (v novější literatuře \(R_n\)). Za mezí pevnosti dochází ke zužování průřezu (tzv. tvorbě krčku) a v bodě \(T\) dojde k přetržení vzorku.
Křehký materiál
Namáhání těles
Působení vnějších sil na těleso může být různé. Hovoříme pak o namáhání tělesa v tahu, v tlaku, v ohybu, ve smyku, v kroucení, ve střihu apod.
Dopružovnání
U některých materiálů nezmizí po odstranění zatížení deformace ihned, ale pouze její část. Zbytek deformace pak mizí po určitou dobu. Tento jev se nazývá dopružování (elastická hystereze). Dopružování a odchylky od Hookova zákona se objevují při opakovaném namáhání materiálu tahem a tlakem. Křivky napínání a stlačování pak vytváří tzv. hysterezní křivku.
Literatura
- HÁJEK, E., REIF, P., VALENTA, F.: Pružnost a pevnost I. 1. vyd. Praha : SNTL/ALFA, 1988. 432 s.
- HÁJEK, E. a kol.: Pružnost a pevnost I.. 1. vyd. Praha : ČVUT, 1981. 444 s.
- HÁJEK, E. a kol.: Pružnost a pevnost II.. 1. vyd. Praha : ČVUT, 1981. 252 s. : 344 obr.
- ZEMAN, V., LAŠ, V.: Technická mechanika. 3. vyd. Plzeň : Vydavatelství ZČU v Plzni, 2001. 191 s.
- LAŠ, V., HLAVÁČ, V., VACEK, V.: Technická mechanika v příkladech. 5. vyd. Plzeň : Vydavatelství ZČU v Plzni, 2009. 160 s.
Související články
Reference
- ↑ 1,0 1,1 1,2 PLÁNIČKA, F.; ZAJÍČEK, M.; ADÁMEK, V. Podpůrné materiály pro studium předmětu Pružnost a pevnost 1 : Shrnutí základních poznatků [online]. Plzeň : Fakulta aplikovaných věd, 2007 [cit. 2010-02-21]. Tah - tlak, s. . Dostupné z WWW: <http://www.kme.zcu.cz/kmet/pp/tah-tlak/shrnuti.pdf>.
- ↑ BARTUŠKA, Karel; SVOBODA, Emanuel. Molekulová fyzika a termika. 4. vyd. Praha : Prometheus, 2005. 244 s. ISBN 80-7196-200-7. Strana 138.
- ↑ DROZD, Zdeněk. FyzWeb [online]. 2001 [cit. 2010-04-02]. Deformační zkouška - cesta k poznání mechanických vlastností materiálů. Dostupné z WWW: <http://fyzweb.cuni.cz/knihovna/deformace/index.htm#12>
Externí odkazy
- Podpůrné materiály pro studium předmětu Pružnost a pevnost I (obsahuje problémy rozdělené do osmi kapitol s řešenými a interaktivními příklady)
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |