Obdélník

Z Multimediaexpo.cz

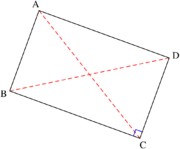
Obdélník s vyznačenými úhlopříčkami

Obdélník o stranách 4×5

Obdélník je rovnoběžník, který má všechny úhly pravé.

Vlastnosti

Vzájemně protilehlé strany jsou rovnoběžné a mají shodnou délku.
Úhlopříčky obdélníka se půlí a jsou stejně dlouhé.
Obdélník má kružnici opsanou se středem v průsečíku úhlopříček a poloměrem rovným polovině délky úhlopříčky.
Obdélník obecně nemá kružnici vepsanou – výjimkou je pouze speciální případ obdélníka – čtverec.
Obdélník je středově souměrný podle průsečíku úhlopříček.
Obdélník je v obecném případě osově souměrný podle dvou os. Osami souměrnosti jsou rovnoběžky se stranami procházející průsečíkem úhlopříček. Speciální případ obdélníka - čtverec - je osově souměrný podle čtyř os, dalšími dvěma osami jsou jeho úhlopříčky.

Vzorce

Pokud označíme \( a,b \,\! \) délky stran, \( u \,\! \) délku úhlopříčky, \( r \,\! \) poloměr kružnice opsané, \( S \,\! \) obsah a \( o \,\! \) obvod obdélníka, pak platí následující vztahy:

\(S=ab \,\!\)
\(u=\sqrt{a^2+b^2}\) (Pythagorova věta)
\(r=\frac{u}{2}\)
\(o=2a+2b \,\!\)

Související články

Commons nabízí fotografie, obrázky a videa k tématu
Obdélník

Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010
Informace o článku. Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. Tento text je dostupný za podmínek Creative Commons 3.0 Unported – creativecommons.org. Originální článek na české Wikipedii