Multimediaexpo.cz je již 18 let na českém internetu !!
V tiskové zprávě k 18. narozeninám brzy najdete nové a zásadní informace.
Brahmaguptův vzorec
Z Multimediaexpo.cz
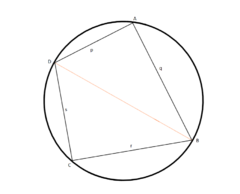
Brahmaguptův vzorec, podle indického matematika Brahmagupty (* 598, † 668), umožňuje vypočítat obsah S tětivového čtyřúhelníka, tedy takového, kterému může být opsána kružnice.
Nechť ABCD je tětivový čtyřúhelník se stranami a, b, c a d, pak platí:
- \(S=\sqrt{(s-a)(s-b)(s-c)(s-d)}\),
kde s je polovina obvodu tohoto čtyřúhelníka:
- \(s=\frac{a+b+c+d}{2}.\)
Pokud se jedna ze stran rovná nule, dostaneme Heronův vzorec pro trojúhelník:
- \( S = \sqrt{ s(s-a)(s-b)(s-c)}.\)
Brahmaguptův vzorec lze dokázat aplikací Heronova vzorce na dva trojúhelníky, na které lze čtyřúhelník rozdělit.
Zobecněním Brahmaguptova vzorce na obecné rovinné čtyřúhelníky je Bretschneiderův vzorec.
- \(S=\sqrt{(s-a)(s-b)(s-c)(s-d)-abcd\cos^2\theta},\)
kde \(\theta\) je polovina součtu dvou protilehlých úhlů čtyřúhelníka.
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |