V sobotu 2. listopadu proběhla mohutná oslava naší plnoletosti !!
Multimediaexpo.cz je již 18 let na českém internetu !!

Ostroúhlý trojúhelník

Z Multimediaexpo.cz

(Rozdíly mezi verzemi)
m (1 revizi)
(+ Masivní vylepšení)
 
Řádka 1: Řádka 1:
-
{{Wikipedia-cs|Ostroúhlý trojúhelník|700}}
+
[[Soubor:OstrouhlyTrojuhelnik.jpg|240px|right]]
 +
'''Ostroúhlý trojúhelník''' je [[trojúhelník]], jehož všechny [[Trojúhelník#Základní pojmy|vnitřní úhly]] jsou [[Úhel#Druhy úhlů|ostré]].
 +
==Vlastnosti==
 +
 +
To, že trojúhelník má všechny vnitřní úhly ostré, ovlivní tyto vlastnosti:
 +
 +
*Všechny [[Trojúhelník#Výšky, těžnice a střední příčky|výšky]] leží uvnitř trojúhelníku.
 +
*Střed [[Trojúhelník#Kružnice opsaná a vepsaná|kružnice opsané]] (průsečík os stran) leží uvnitř trojúhelníku.
 +
*Druhá mocnina libovolné strany je vždy menší než součet druhých mocnin zbývajících dvou stran:
 +
:např. ''c''<sup>2</sup> < ''a''<sup>2</sup> + ''b''<sup>2</sup> , kde ''a'', ''b'', ''c'' jsou strany trojúhelníka
 +
 +
 +
[[Soubor:VlastnostiOstrouhlehoTrojuhelnika.jpg|575px|left]]
 +
<br style="clear: both;" />
 +
==Související články==
 +
*[[Rovinné geometrické útvary]]
 +
*[[Mnohoúhelník]]
 +
*[[Trojúhelník]]
 +
*[[Rovnostranný trojúhelník]]
 +
*[[Rovnoramenný trojúhelník]]
 +
 +
 +
{{Článek z Wikipedie}}
[[Kategorie:Trojúhelník]]
[[Kategorie:Trojúhelník]]

Aktuální verze z 24. 10. 2014, 10:15

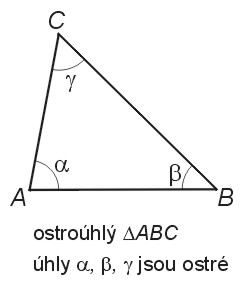
OstrouhlyTrojuhelnik.jpg

Ostroúhlý trojúhelník je trojúhelník, jehož všechny vnitřní úhly jsou ostré.

Vlastnosti

To, že trojúhelník má všechny vnitřní úhly ostré, ovlivní tyto vlastnosti:

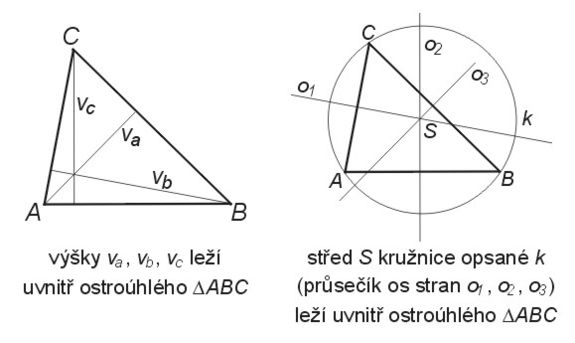
  • Všechny výšky leží uvnitř trojúhelníku.
  • Střed kružnice opsané (průsečík os stran) leží uvnitř trojúhelníku.
  • Druhá mocnina libovolné strany je vždy menší než součet druhých mocnin zbývajících dvou stran:
např. c2 < a2 + b2 , kde a, b, c jsou strany trojúhelníka


VlastnostiOstrouhlehoTrojuhelnika.jpg


Související články


Citováno z „http://ww2000w.multimediaexpo.cz/mmecz/index.php/Ostro%C3%BAhl%C3%BD_troj%C3%BAheln%C3%ADk“