Multimediaexpo.cz je již 18 let na českém internetu !!
Průměr (geometrie)
Z Multimediaexpo.cz
(+ Vylepšení) |
m (Nahrazení textu „<math>“ textem „<big>\(“) |
||
| Řádka 4: | Řádka 4: | ||
Výrazem průměr označujeme i délku této úsečky. Rovná se dvojnásobku [[poloměr]]u ''r'': | Výrazem průměr označujeme i délku této úsečky. Rovná se dvojnásobku [[poloměr]]u ''r'': | ||
| - | :< | + | :<big>\(d = 2.r</math> |
Průměr kružnice nebo kruhu je roven podílu [[obvod]]u a čísla ''[[číslo pí|π]]'': | Průměr kružnice nebo kruhu je roven podílu [[obvod]]u a čísla ''[[číslo pí|π]]'': | ||
| - | :< | + | :<big>\(d = \frac{O}{\pi}</math> |
==Obecná definice== | ==Obecná definice== | ||
Obecně lze průměr [[Množina|množiny]] ''M'' [[bod]]ů [[metrický prostor|metrického prostoru]] definovat jako [[supremum]] množiny všech hodnot ''l'' takových, že ''l'' je [[vzdálenost]] nějakých dvou bodů v ''M''. Formálně | Obecně lze průměr [[Množina|množiny]] ''M'' [[bod]]ů [[metrický prostor|metrického prostoru]] definovat jako [[supremum]] množiny všech hodnot ''l'' takových, že ''l'' je [[vzdálenost]] nějakých dvou bodů v ''M''. Formálně | ||
| - | :< | + | :<big>\(d = sup \{ \rho (x,y); x, y \in\mathbb{M} \}</math> |
kde ''ρ'' je [[metrika]] na daném prostoru. | kde ''ρ'' je [[metrika]] na daném prostoru. | ||
Verze z 14. 8. 2022, 14:49
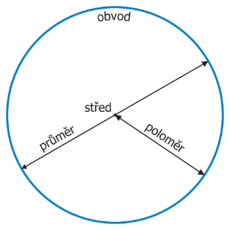
Průměr kružnice je úsečka, která prochází středem kružnice a jejíž oba krajní body leží na této kružnici. Analogicky lze definovat průměr kruhu a koule. Označuje se písmenem d (zkr. diameter), případně symbolem ⌀ (viz níže).
Výrazem průměr označujeme i délku této úsečky. Rovná se dvojnásobku poloměru r:
- \(d = 2.r</math>
Průměr kružnice nebo kruhu je roven podílu obvodu a čísla π:
- \(d = \frac{O}{\pi}</math>
Obecná definice
Obecně lze průměr množiny M bodů metrického prostoru definovat jako supremum množiny všech hodnot l takových, že l je vzdálenost nějakých dvou bodů v M. Formálně
- \(d = sup \{ \rho (x,y); x, y \in\mathbb{M} \}</math>
kde ρ je metrika na daném prostoru.
Číslo d není definováno jako maximum, neboť některé množiny neobsahují vlastní hranici a uvedená množina tak nemá největší hodnotu. V případě uzavřených konvexních množin je průměr roven délce nejdelší úsečky, která leží v M. Např. průměr krychle je roven délce její tělesové úhlopříčky, průměr trojúhelníka jeho nejdelší straně.
Značení
Symbol '⌀', který lze zhruba popsat jako šikmo přeškrtnutou kružnici, má v Unicode tabulce číslo 8960 (2300 v šestnáctkové soustavě). V HTML jej lze zapsat jako ⌀ nebo ⌀. Mnoho fontů však tento symbol neobsahuje, proto je na webu občas místo něj použito přeškrtnuté malé ó 'ø', případně znak pro prázdnou množinu '∅', případně řecké písmeno Fí 'Φ', což jsou sice jiné symboly, ale svojí podobou znak pro průměr připomínají.
V LaTeXu se tento symbol píše příkazem \diameter.
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |