Multimediaexpo.cz je již 18 let na českém internetu !!
Trojúhelníkové číslo
Z Multimediaexpo.cz
(+ Aktualizace) |
m (Nahrazení textu „</math>“ textem „\)</big>“) |
||
| (Není zobrazena jedna mezilehlá verze.) | |||
| Řádka 1: | Řádka 1: | ||
[[Soubor:First six triangular numbers.png|thumb|240px|Z počtů bodů daných trojúhelníkovými čísly lze sestavit [[trojúhelník]]ové obrazce]] | [[Soubor:First six triangular numbers.png|thumb|240px|Z počtů bodů daných trojúhelníkovými čísly lze sestavit [[trojúhelník]]ové obrazce]] | ||
'''Trojúhelníkové číslo''' je v [[matematika|matematice]] [[sčítání|součet]] ''n'' [[přirozené číslo|přirozených čísel]] od 1 do ''n''. | '''Trojúhelníkové číslo''' je v [[matematika|matematice]] [[sčítání|součet]] ''n'' [[přirozené číslo|přirozených čísel]] od 1 do ''n''. | ||
| - | < | + | <big>\( |
T_n= 1+2+3+ \dotsb +(n-1)+n = \frac{n(n+1)}{2} = \frac{n^2+n}{2} \overset{\underset{\mathrm{def}}{}} {=} {n+1 \choose 2} | T_n= 1+2+3+ \dotsb +(n-1)+n = \frac{n(n+1)}{2} = \frac{n^2+n}{2} \overset{\underset{\mathrm{def}}{}} {=} {n+1 \choose 2} | ||
| - | </ | + | \)</big> |
Jak je vidět z pravého konce tohoto vzorce, každé trojúhelníkové číslo je zároveň [[kombinační číslo|kombinačním číslem]]. | Jak je vidět z pravého konce tohoto vzorce, každé trojúhelníkové číslo je zároveň [[kombinační číslo|kombinačním číslem]]. | ||
Aktuální verze z 14. 8. 2022, 14:54
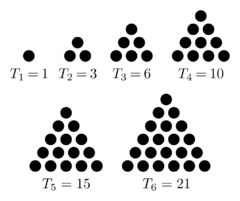
Trojúhelníkové číslo je v matematice součet n přirozených čísel od 1 do n. \( T_n= 1+2+3+ \dotsb +(n-1)+n = \frac{n(n+1)}{2} = \frac{n^2+n}{2} \overset{\underset{\mathrm{def}}{}} {=} {n+1 \choose 2} \)
Jak je vidět z pravého konce tohoto vzorce, každé trojúhelníkové číslo je zároveň kombinačním číslem.
Posloupnost trojúhelníkových čísel v OEIS) pro n = 1, 2, 3… je: [1]
Jeden z prvních, kdo používal trojúhelníková čísla, byl Karl Friedrich Gauss (1777 – 1855), který je použil ve škole, když mu bylo devět let. Učitel žákům udělil práci, ve které měli počítat 1+2+3+…+1000.
Po chvíli se Karl Gauss přihlásil se správným řešením. Udělal to tak, že vypočítal 1000·1001:2 = 500500.
Reference
- ↑ Posloupnost A000217 v databázi On-Line Encyclopedia of Integer Sequences.
Externí odkazy
|
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |