Multimediaexpo.cz je již 18 let na českém internetu !!
Gaussův integrál
Z Multimediaexpo.cz
m (1 revizi) |
(+ Masivní vylepšení) |
||
| Řádka 1: | Řádka 1: | ||
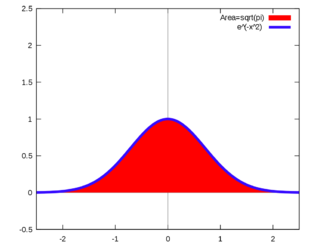
| - | + | [[Soubor:E^(-x^2).png|thumb|310px|Graf ''ƒ''(''x'') = ''e''<sup>−''x''<sup>2</sup></sup> a plochy mezi funkcí a osou ''x''; tato plocha se rovná <math> \scriptstyle\sqrt{\pi} </math>]] | |
| + | '''Gaussův integrál''', také známý jako '''Eulerův-Poissonův integrál''' či '''Poissonův integrál''',<ref>[http://slovari.yandex.ru/dict/bse/article/00063/81000.htm Пуассона интеграл], БСЭ</ref> je [[integrál]] [[Gaussova funkce|Gaussovy funkce]] ''e''<sup>−''x''<sup>2</sup></sup> přes celou reálnou osu, tedy | ||
| + | |||
| + | :<math>\int_{-\infty}^\infty e^{-x^2}\,dx = \sqrt{\pi}.</math> | ||
| + | |||
| + | Jména tomuto integrálu dali matematici [[Carl Friedrich Gauss]], [[Leonhard Euler]] a [[Siméon Denis Poisson]]. | ||
| + | |||
| + | == Výpočet == | ||
| + | Integrál [[Gaussova funkce|Gaussovy funkce]] označíme <math>Y</math>. | ||
| + | :<math>Y = \int_{-\infty}^\infty \mathrm{e}^{-x^2} \mathrm{d}x</math> | ||
| + | |||
| + | Obě strany rovnice umocníme na druhou, přičemž proměnnou ve druhém integrálu označíme <math>y</math>. | ||
| + | :<math>Y^2 = \int_{-\infty}^\infty \mathrm{e}^{-x^2} \mathrm{d}x \int_{-\infty}^\infty \mathrm{e}^{-y^2} \mathrm{d}y</math> | ||
| + | |||
| + | Součin integrálů odpovídá dvojnému integrálu funkce dvou proměnných, která je součinem původních funkcí. | ||
| + | |||
| + | :<math>Y^2 = \int_{-\infty}^\infty \int_{-\infty}^\infty \mathrm{e}^{-x^2}\mathrm{e}^{-y^2} \mathrm{d}x\mathrm{d}y = \int_{-\infty}^\infty \int_{-\infty}^\infty \mathrm{e}^{-(x^2+y^2)} \mathrm{d}x\mathrm{d}y</math> | ||
| + | |||
| + | [[Graf funkce|Graf]] této funkce si můžeme představit jako kopec (tvarem připomíná horu [[Říp]]) nad rovinou s kartézskými souřadnicemi <math>(x,y)</math>. Integrál představuje [[objem]] kopce. Jelikož je kopec souměrný podle svislé osy, hodí se k jeho popisu [[polární soustava souřadnic]] <math>(\varphi,r)</math>, do kterých funkci přepíšeme. | ||
| + | |||
| + | :<math>Y^2 = \int_0^{2\pi} \int_0^\infty r \mathrm{e}^{-r^2} \mathrm{d}\varphi\mathrm{d}r = \int_0^{2\pi}\mathrm{d}\varphi \int_0^\infty r \mathrm{e}^{-r^2} \mathrm{d}r</math> | ||
| + | Tento integrál už lze jednoduše vyčíslit nalezením primitivní funkce metodou [[per partes]] a jeho hodnota je <math>\pi</math>. Odmocněním rovnice dostaneme výsledek. | ||
| + | :<math>Y = \sqrt{\pi}</math> | ||
| + | |||
| + | == Reference == | ||
| + | <references /> | ||
| + | == Externí odkazy == | ||
| + | * Kvasnica J.: Matematický aparát fyzika | ||
| + | |||
| + | |||
| + | {{Článek z Wikipedie}} | ||
[[Kategorie:Integrální počet]] | [[Kategorie:Integrální počet]] | ||
Verze z 19. 9. 2014, 07:51
Gaussův integrál, také známý jako Eulerův-Poissonův integrál či Poissonův integrál,[1] je integrál Gaussovy funkce e−x2 přes celou reálnou osu, tedy
- <math>\int_{-\infty}^\infty e^{-x^2}\,dx = \sqrt{\pi}.</math>
Jména tomuto integrálu dali matematici Carl Friedrich Gauss, Leonhard Euler a Siméon Denis Poisson.
Výpočet
Integrál Gaussovy funkce označíme <math>Y</math>.
- <math>Y = \int_{-\infty}^\infty \mathrm{e}^{-x^2} \mathrm{d}x</math>
Obě strany rovnice umocníme na druhou, přičemž proměnnou ve druhém integrálu označíme <math>y</math>.
- <math>Y^2 = \int_{-\infty}^\infty \mathrm{e}^{-x^2} \mathrm{d}x \int_{-\infty}^\infty \mathrm{e}^{-y^2} \mathrm{d}y</math>
Součin integrálů odpovídá dvojnému integrálu funkce dvou proměnných, která je součinem původních funkcí.
- <math>Y^2 = \int_{-\infty}^\infty \int_{-\infty}^\infty \mathrm{e}^{-x^2}\mathrm{e}^{-y^2} \mathrm{d}x\mathrm{d}y = \int_{-\infty}^\infty \int_{-\infty}^\infty \mathrm{e}^{-(x^2+y^2)} \mathrm{d}x\mathrm{d}y</math>
Graf této funkce si můžeme představit jako kopec (tvarem připomíná horu Říp) nad rovinou s kartézskými souřadnicemi <math>(x,y)</math>. Integrál představuje objem kopce. Jelikož je kopec souměrný podle svislé osy, hodí se k jeho popisu polární soustava souřadnic <math>(\varphi,r)</math>, do kterých funkci přepíšeme.
- <math>Y^2 = \int_0^{2\pi} \int_0^\infty r \mathrm{e}^{-r^2} \mathrm{d}\varphi\mathrm{d}r = \int_0^{2\pi}\mathrm{d}\varphi \int_0^\infty r \mathrm{e}^{-r^2} \mathrm{d}r</math>
Tento integrál už lze jednoduše vyčíslit nalezením primitivní funkce metodou per partes a jeho hodnota je <math>\pi</math>. Odmocněním rovnice dostaneme výsledek.
- <math>Y = \sqrt{\pi}</math>
Reference
- ↑ Пуассона интеграл, БСЭ
Externí odkazy
- Kvasnica J.: Matematický aparát fyzika
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |