Multimediaexpo.cz je již 18 let na českém internetu !!
Povrchové napětí
Z Multimediaexpo.cz
m (Nahrazení textu „<math>“ textem „<big>\(“) |
m (Nahrazení textu „</math>“ textem „\)</big>“) |
||
| Řádka 11: | Řádka 11: | ||
Zvětšíme-li plochu nějaké kapaliny, musíme vykonat [[Práce (fyzika)|práci]] právě kvůli povrchovému napětí. Povrchové napětí je tedy tak i definováno jako práce potřebná k zvětšení plochy vydělena plochou, která při tom vznikne navíc. Povrchové napětí tedy může být označeno i jako hustota povrchové energie. Při zvětšování povrchu musí být vyvinuta [[síla]], například když se pohybem smyčky z drátu směrem vzhůru, pokusíme zvětšit blánu, která se na smyčce vytvoří. Síla je úměrná délce smyčky a pro tekutiny je tato síla rovna změně povrchové energie. | Zvětšíme-li plochu nějaké kapaliny, musíme vykonat [[Práce (fyzika)|práci]] právě kvůli povrchovému napětí. Povrchové napětí je tedy tak i definováno jako práce potřebná k zvětšení plochy vydělena plochou, která při tom vznikne navíc. Povrchové napětí tedy může být označeno i jako hustota povrchové energie. Při zvětšování povrchu musí být vyvinuta [[síla]], například když se pohybem smyčky z drátu směrem vzhůru, pokusíme zvětšit blánu, která se na smyčce vytvoří. Síla je úměrná délce smyčky a pro tekutiny je tato síla rovna změně povrchové energie. | ||
[[Soubor:Povrchove_napeti.png|thumb|Povrchové napětí.]] | [[Soubor:Povrchove_napeti.png|thumb|Povrchové napětí.]] | ||
| - | Jako povrchové napětí lze označit [[síla|sílu]], která působí [[kolmost|kolmo]] na délku myšleného [[rovinný řez|řezu]] povrchem, dělenou touto [[délka|délkou]], a která leží v [[tečná rovina|tečné rovině]] k povrchu v daném bodě. Pokud působí na [[úsečka|úsečku]] délky <big>\(\mathrm{d}l</ | + | Jako povrchové napětí lze označit [[síla|sílu]], která působí [[kolmost|kolmo]] na délku myšleného [[rovinný řez|řezu]] povrchem, dělenou touto [[délka|délkou]], a která leží v [[tečná rovina|tečné rovině]] k povrchu v daném bodě. Pokud působí na [[úsečka|úsečku]] délky <big>\(\mathrm{d}l\)</big> v [[rovina|rovině]] povrchu kolmá síla <big>\(\mathrm{d}F\)</big>, pak povrchové napětí vyjádříme jako |
| - | :<big>\(\sigma = \frac{\mathrm{d}F}{\mathrm{d}l}</ | + | :<big>\(\sigma = \frac{\mathrm{d}F}{\mathrm{d}l}\)</big> |
Z [[:soubor:povrchove_napeti.png|obrázku]] je vidět, že na jednotkovou délku myšleného řezu působí pravá strana povrchové vrstvy napětím σ a levá strana napětím σ′, které je stejně velké, ale působí opačným směrem. Síly působící v myšleném řezu jsou tedy v tomto případě ve vzájemné rovnováze. Na zakřiveném povrchu vzniká působením povrchového napětí tlak, který je kolmý k povrchu kapaliny, a který u konvexního (vypuklého) povrchu směřuje do kapalin, u konkávního (vydutého) povrchu směřuje ven z kapaliny. | Z [[:soubor:povrchove_napeti.png|obrázku]] je vidět, že na jednotkovou délku myšleného řezu působí pravá strana povrchové vrstvy napětím σ a levá strana napětím σ′, které je stejně velké, ale působí opačným směrem. Síly působící v myšleném řezu jsou tedy v tomto případě ve vzájemné rovnováze. Na zakřiveném povrchu vzniká působením povrchového napětí tlak, který je kolmý k povrchu kapaliny, a který u konvexního (vypuklého) povrchu směřuje do kapalin, u konkávního (vydutého) povrchu směřuje ven z kapaliny. | ||
=== Termodynamická definice === | === Termodynamická definice === | ||
Obecná termodynamická definice povrchového napětí zní: | Obecná termodynamická definice povrchového napětí zní: | ||
Povrchové napětí σ („sigma“) je [[derivace]] volné [[entalpie]] G podle [[plocha|plochy]] S při konstantní [[teplota|teplotě]] T a konstantním [[tlak]]u p. | Povrchové napětí σ („sigma“) je [[derivace]] volné [[entalpie]] G podle [[plocha|plochy]] S při konstantní [[teplota|teplotě]] T a konstantním [[tlak]]u p. | ||
| - | <big>\( \sigma = \left(\frac{\partial G}{\partial S} \right)_{T,p} </ | + | <big>\( \sigma = \left(\frac{\partial G}{\partial S} \right)_{T,p} \)</big> |
Volná entalpie má rozměr stejný jako energie. Tudíž σ má rozměr energie/plocha. | Volná entalpie má rozměr stejný jako energie. Tudíž σ má rozměr energie/plocha. | ||
== Jak vzniká povrchové napětí? == | == Jak vzniká povrchové napětí? == | ||
| Řádka 44: | Řádka 44: | ||
[[Soubor:povrchova_energie.png|thumb|Povrchové napětí a povrchová energie.]] | [[Soubor:povrchova_energie.png|thumb|Povrchové napětí a povrchová energie.]] | ||
Ponoříme-li drátěný rámeček s posuvnou příčkou do mýdlového roztoku, vytvoří se na něm vlivem povrchového napětí tenká kapalinová blána. Přestože se nám blána jeví jako jedna vrstva, jde ve skutečnosti o kapalinu, která je sevřena mezi dvěma povrchovými vrstvami. Z toho důvodu má blána vytvořená na drátěném rámečku dvě povrchové vrstvy. | Ponoříme-li drátěný rámeček s posuvnou příčkou do mýdlového roztoku, vytvoří se na něm vlivem povrchového napětí tenká kapalinová blána. Přestože se nám blána jeví jako jedna vrstva, jde ve skutečnosti o kapalinu, která je sevřena mezi dvěma povrchovými vrstvami. Z toho důvodu má blána vytvořená na drátěném rámečku dvě povrchové vrstvy. | ||
| - | Povrchová vrstva působí na otáčivou příčku [[délka|délky]] <big>\(l</ | + | Povrchová vrstva působí na otáčivou příčku [[délka|délky]] <big>\(l\)</big> povrchovým napětím <big>\(\sigma\)</big>, jedna povrchová vrstva tedy působí výslednou silou <big>\(\sigma l\)</big>. Vzhledem k existenci dvou povrchových vrstev udržíme příčku v [[rovnováha sil|rovnováze]] silou <big>\(F = 2\sigma l\)</big>. Při posunutí příčky o [[vzdálenost]] <big>\(\Delta s\)</big> vykonáme [[Práce (fyzika)|práci]] <big>\(W=2\sigma l\Delta s\)</big>, která se jeví jako změna povrchové energie při změně povrchu o <big>\(\Delta S=2l\Delta s\)</big>. Změnu povrchové energie je pak možné vyjádřit jako |
| - | :<big>\(\Delta E = W = \gamma\Delta S</ | + | :<big>\(\Delta E = W = \gamma\Delta S\)</big> |
Z tohoto vztahu vyplývá, že snaha povrchového napětí o [[minimum|minimalizaci]] velikosti povrchu odpovídá minimalizaci povrchové energie. Kapalina se tedy snaží zaujmout takový tvar, při které je její povrchová energie (a tedy i velikost povrchu) nejmenší. | Z tohoto vztahu vyplývá, že snaha povrchového napětí o [[minimum|minimalizaci]] velikosti povrchu odpovídá minimalizaci povrchové energie. Kapalina se tedy snaží zaujmout takový tvar, při které je její povrchová energie (a tedy i velikost povrchu) nejmenší. | ||
== Měření povrchového napětí == | == Měření povrchového napětí == | ||
Aktuální verze z 14. 8. 2022, 14:53
Povrchové napětí je efekt, při kterém se povrch kapalin chová jako elastická fólie a snaží se dosáhnout co možná nejhladšího stavu s minimální plochou. To znamená, že se povrch tekutiny snaží dosáhnout stavu s nejmenší energií. Čím větší je povrchové napětí, tím „kulatější“ je kapička této kapaliny. Povrch kapaliny se tedy chová tak, jako by byl tvořen velmi tenkou pružnou vrstvou, která se snaží stáhnout povrch kapaliny tak, aby měl při daném objemu kapaliny co nejmenší plochu. Pokud by na kapalinu nepůsobily vnější síly, měla by kulový tvar, protože koule má ze všech těles stejného objemu nejmenší povrch. Při působení vnějších sil je situace poněkud složitější. Vždy se však volný povrch kapaliny snaží snížit velikost celkového povrchu na co možná nejmenší možnou míru. To je důvod, proč je hladina klidné vody v otevřené nádobě (v gravitačním poli) vodorovná, neboť jakýkoli jiný tvar volné hladiny kapaliny by zvětšil celkový povrch kapaliny. Jsou-li vnější síly velmi malé proti silám povrchového napětí, bude se kapalina snažit zaujmout přibližně kulový tvar. To se děje např. u drobných kapiček tvořících mlhu, u kapek rtuti apod. Povrchové napětí bývá někdy také označováno jako kapilární konstanta.
Obsah |
Význam povrchového napětí
Povrchové napětí způsobuje, že některé druhy hmyzu (například vodoměrky) se mohou pohybovat po vodní hladině. Objekt, který by vodní hladinu prorazil, by se nutně potopil. Některé předměty, např. žiletky nebo kousek alobalu, lze položit na vodní hladinu, aniž by se potopily; když je ale potopíme dostatečně hluboko, klesnou až na dno. Velké povrchové napětí ztěžuje proces smáčení. Například destilovaná voda smáčí látky obsažené v oblečení velmi špatně, perlí. Toto je jeden z důvodů, proč se při praní přidávají prací prostředky, které svými mýdlovými látkami (tenzidy) smáčení usnadňují. Jiným příkladem je mytí mastných rukou. Mytí mastných rukou je obtížné, protože voda nesmáčí mastný povrch. Proto používáme mýdlo. V mýdlovém roztoku jsou síly mezi molekulami menší než síly mezi molekulami vody. Důsledkem je jednak snížení povrchového napětí vody, jednak to, že roztok smáčí mastný povrch.
Co je povrchové napětí?
Zvětšíme-li plochu nějaké kapaliny, musíme vykonat práci právě kvůli povrchovému napětí. Povrchové napětí je tedy tak i definováno jako práce potřebná k zvětšení plochy vydělena plochou, která při tom vznikne navíc. Povrchové napětí tedy může být označeno i jako hustota povrchové energie. Při zvětšování povrchu musí být vyvinuta síla, například když se pohybem smyčky z drátu směrem vzhůru, pokusíme zvětšit blánu, která se na smyčce vytvoří. Síla je úměrná délce smyčky a pro tekutiny je tato síla rovna změně povrchové energie.
Jako povrchové napětí lze označit sílu, která působí kolmo na délku myšleného řezu povrchem, dělenou touto délkou, a která leží v tečné rovině k povrchu v daném bodě. Pokud působí na úsečku délky \(\mathrm{d}l\) v rovině povrchu kolmá síla \(\mathrm{d}F\), pak povrchové napětí vyjádříme jako
- \(\sigma = \frac{\mathrm{d}F}{\mathrm{d}l}\)
Z obrázku je vidět, že na jednotkovou délku myšleného řezu působí pravá strana povrchové vrstvy napětím σ a levá strana napětím σ′, které je stejně velké, ale působí opačným směrem. Síly působící v myšleném řezu jsou tedy v tomto případě ve vzájemné rovnováze. Na zakřiveném povrchu vzniká působením povrchového napětí tlak, který je kolmý k povrchu kapaliny, a který u konvexního (vypuklého) povrchu směřuje do kapalin, u konkávního (vydutého) povrchu směřuje ven z kapaliny.
Termodynamická definice
Obecná termodynamická definice povrchového napětí zní: Povrchové napětí σ („sigma“) je derivace volné entalpie G podle plochy S při konstantní teplotě T a konstantním tlaku p. \( \sigma = \left(\frac{\partial G}{\partial S} \right)_{T,p} \) Volná entalpie má rozměr stejný jako energie. Tudíž σ má rozměr energie/plocha.
Jak vzniká povrchové napětí?
Povrchové napětí je výsledkem vzájemné interakce přitažlivých sil molekul nebo atomů, z nichž se skládá povrchová vrstva. Pozorujeme-li povrchovou vrstvu resp. rozhraní jako nějaký řez, pak lze povrchové napětí chápat také jako energii nenasycených vazeb na jednotku plochy (koheze). Povrchové napětí ale nemá pro makroskopické systémy funkci povrchové geometrie.
Příčina: přitažlivé síly
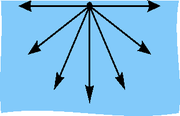
Napravo je schematicky znázorněno, že přitažlivé síly působí na povrchovou částici asymetricky. Podobné obrázky se používají jako ilustrace k vysvětlení povrchového napětí. Neměly by ale být špatně interpretovány.
Co toto schéma správně znázorňuje
- Povrchové napětí vzniká vzájemným působením přitažlivých sil mezi částicemi tekutého tělesa; Tyto jsou silnější než síly mezi dvěma částicemi plynu nebo částicí kapaliny a plynu.
- Důvodem k vzniku povrchového napětí je zlom v symetrii na povrchu ve srovnání s vnitřkem kapaliny a vnitřkem plynu.
Pozor na chybné interpretace
Povrchové napětí působí přímo v povrchu, ne kolmo k němu! Vzniká sice silami, které jsou schematicky znázorněny na obrázku, jejich směr však nelze jednoduše vyjádřit jako součet znázorněných sil. Schéma znázorňuje jen přitažlivé síly. Mezi dvěma částicemi působí ale i odpudivé síly, které se projeví až při větším přiblížení těchto částic. V rovnovážném stavu neexistují žádné výsledné síly, které působí směrem do vnitřku kapaliny! Kdyby se taková síla vyskytla, částice by byla urychlována do vnitřku kapaliny, než by se projevily odpudivé síly. Z toho vyplývá, že střední vzdálenost povrchových molekul je větší a tím vzniká i odlišná hustota ve srovnání s vnitřkem kapaliny: Z důvodu neustálého pohybu částic v kapalině je střední vzájemný rovnovážný odstup na povrchu větší a hustota je menší. Zmenšení povrchu vede spíše k zisku energie a ten je důvodem pro vznik povrchového napětí. Povrchové napětí je také vlastnost, která se vyskytuje při termodynamické rovnováze. Tedy když je tekutina v rovnováze se svými párami. Pak se nemění pozice fázové hranice a na částice nepůsobí žádné síly ve směru kolmo k fázové hranici. To znamená, že částice není urychlována ani do vnitřku kapaliny, ani do vnitřku plynu, a to nezávisle na tom, kde se nachází. Samozřejmě při rovnovážném stavu neexistují žádné síly, které by urychlovaly povrchové částice.
Důsledky povrchového napětí
Ve snaze snížit povrchovou energii, tedy nasytit všechny volné vazby v povrchové vrstvě, se zmenšuje povrch kapalin. Protože má koule ze všech těles nejmenší povrch, snaží se kapaliny, na které nepůsobí žádné další síly (jako například ve stavu beztíže) zaujmout kulový tvar. V kapičce kapaliny, například v malé kapce vody nebo plynové bublině uvnitř kapaliny, působí kvůli povrchovému napětí na rozhraní kapalina/plyn zvýšený tlak, taktéž i ve vnitřku mýdlové bubliny. Zvýšení tlaku popisuje Young-Laplaceova rovnice.
Sedmikráska (chudobka) je pod vodou, která ji nadnáší. Před ponořením jí brání právě povrchové napětí, které neumožňuje vodě protéci mezi okvětními plátky a květ zatopit. |
Kovová kancelářská sponka může splývat na vodní hladině, pokud je na ni opatrně položena. |
Povrchová energie
V důsledku existence povrchového napětí je v povrchové vrstvě nahromaděna i jistá energie, tzv. povrchová energie.
Ponoříme-li drátěný rámeček s posuvnou příčkou do mýdlového roztoku, vytvoří se na něm vlivem povrchového napětí tenká kapalinová blána. Přestože se nám blána jeví jako jedna vrstva, jde ve skutečnosti o kapalinu, která je sevřena mezi dvěma povrchovými vrstvami. Z toho důvodu má blána vytvořená na drátěném rámečku dvě povrchové vrstvy. Povrchová vrstva působí na otáčivou příčku délky \(l\) povrchovým napětím \(\sigma\), jedna povrchová vrstva tedy působí výslednou silou \(\sigma l\). Vzhledem k existenci dvou povrchových vrstev udržíme příčku v rovnováze silou \(F = 2\sigma l\). Při posunutí příčky o vzdálenost \(\Delta s\) vykonáme práci \(W=2\sigma l\Delta s\), která se jeví jako změna povrchové energie při změně povrchu o \(\Delta S=2l\Delta s\). Změnu povrchové energie je pak možné vyjádřit jako
- \(\Delta E = W = \gamma\Delta S\)
Z tohoto vztahu vyplývá, že snaha povrchového napětí o minimalizaci velikosti povrchu odpovídá minimalizaci povrchové energie. Kapalina se tedy snaží zaujmout takový tvar, při které je její povrchová energie (a tedy i velikost povrchu) nejmenší.
Měření povrchového napětí
Povrchové napětí lze měřit například kroužkovou (podle Lecomta de Noüy) nebo žehlící metodou (podle Lenarda), Tenziometrem, Stalagmometrem nebo metodou kapilární elevace (popř. deprese).
Hodnoty povrchového napětí
Hodnota povrchového napětí vody při 20 °C činí asi 0,073N/m. Tabulková hodnota pro povrchové napětí při 20 °C.
| kapalina | σ [10-3N/m] |
|---|---|
| aceton | 23,3 |
| benzen | 28,9 |
| etanol | 22,55 |
| n-hexan | 18,4 |
| n-pentan | 16,0 |
| rtuť | 476 |
| voda | 72,75 |
Z tabulky je zřejmé, že voda má poměrně vysoké povrchové napětí. Jen rtuť má podstatně více.
Závislost povrchového napětí na složení a teplotě
Povrchově aktivní látky snižují hodnotu povrchového napětí; jejich efekt lze popsat laterálním tlakem π, který působí proti povrchovému napětí. π není žádný skutečný tlak, nýbrž má jen stejnou jednotku jako povrchové napětí. Je-li hraničící vzduchová vrstva nasycena plyny kapaliny, pak může pronikání dalších par z vnějšku výrazně ovlivnit povrchové napětí. Povrchové napětí je silně závislé na teplotě a všeobecně platí, že klesá s rostoucí teplotou. Od kritického bodu je rovno nule.
Z historie
Pojem povrchového napětí byl poprvé použit roku 1629 vědcem N. Cabeo a 1751 Segnerem blíže vysvětlen. K vzniku teorie významně přispěli 1805 Thomas Young, 1806 Pierre Simon de Laplace a 1830 Segner Poisson. Viz Young-Laplaceova rovnice.
Související články
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |