Gravitační zrychlení

Z Multimediaexpo.cz

(Rozdíly mezi verzemi)

Aktuální verze z 14. 8. 2022, 14:51

Gravitační zrychlení je zrychlení, které tělesu udílí gravitační síla.

Značka: a_g

Vztah gravitačního a tíhového zrychlení

Gravitační zrychlení vyjadřuje intenzitu gravitačního pole v daném místě, ve kterém se projevuje gravitační působení hmotných těles. Vyjadřuje gravitační sílu, kterou toto pole působí na bodové těleso o jednotkové hmotnosti.

Gravitační a tíhové zrychlení na zemském povrchu

Teoretická střední hodnota gravitačního zrychlení na povrchu Země je a_g = 9,823 m·s^-2. Tato hodnota vyplývá ze vztahu pro intenzitu gravitačního pole \(a_g = \varkappa\frac{M}{R^2}\) po dosazení hodnot poloměru a hmotnosti \(M \,\) Země, za zjednodušujícího předpokladu, že Země je nehybná, homogenní, dokonalá koule o poloměru \(R \,\) = 6371 km, což je poloměr koule o stejném objemu jako je skutečný objem Země. S gravitačním zrychlením by tělesa padala k Zemi, kdyby se Země neotáčela.

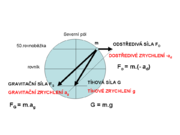
Na tělesa otáčející se spolu se Zemí (tedy ve vztažné soustavě spojené s povrchem Země) působí výslednice dvou sil: gravitační síly a odstředivé síly. Tato výslednice se nazývá tíhová síla a uděluje tělesům při volném pádu tíhové zrychlení, což je vektorová výslednice gravitačního zrychlení a odstředivého zrychlení.

Tíhové zrychlení vyjadřuje intenzitu tíhového pole na povrchu Země. Na různých místech zemského povrchu se velikost tíhového zrychlení mírně liší (v řádu setin m·s^-2); na rovníku je jeho hodnota menší a směrem k pólům se zvětšuje. To je způsobeno velikostí odstředivé síly vznikající rotací Země, která je největší na rovníku a nejmenší na pólech. Dohodnutá střední hodnota tíhového zrychlení, tzv. normální tíhové zrychlení, je g = 9,80665 m·s^-2.

Na povrchu Měsíce je gravitační zrychlení přibližně šestkrát menší než na Zemi.

Literatura

Bednařík,Široká:Mechanika,Prometheus 2000,ISBN 80-7196-176-0

Související články

Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010
Informace o článku. Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. Tento text je dostupný za podmínek Creative Commons 3.0 Unported – creativecommons.org. Originální článek na české Wikipedii

@@ Řádka 9: / Řádka 9: @@
 ==Gravitační a tíhové zrychlení na zemském povrchu==
-Teoretická střední hodnota gravitačního zrychlení na povrchu [[Země]] je ''a''<sub>g</sub>&nbsp;=&nbsp;9,823&nbsp;m·s<sup>-2</sup>. Tato hodnota vyplývá ze vztahu pro [[Intenzita gravitačního pole|intenzitu gravitačního pole]] <math>a_g = \varkappa\frac{M}{R^2}</math> po dosazení hodnot poloměru a hmotnosti <math>M \,</math> Země, za zjednodušujícího předpokladu, že Země je nehybná, homogenní, dokonalá koule o poloměru <math>R \,</math>&nbsp;=&nbsp;6371&nbsp;km, což je [[Koule#Vlastnosti|poloměr koule o stejném objemu]] jako je skutečný [[Země|objem Země]]. S gravitačním zrychlením by tělesa padala k Zemi, kdyby se Země neotáčela.
+Teoretická střední hodnota gravitačního zrychlení na povrchu [[Země]] je ''a''<sub>g</sub>&nbsp;=&nbsp;9,823&nbsp;m·s<sup>-2</sup>. Tato hodnota vyplývá ze vztahu pro [[Intenzita gravitačního pole|intenzitu gravitačního pole]] <big>\(a_g = \varkappa\frac{M}{R^2}\)</big> po dosazení hodnot poloměru a hmotnosti <big>\(M \,\)</big> Země, za zjednodušujícího předpokladu, že Země je nehybná, homogenní, dokonalá koule o poloměru <big>\(R \,\)</big>&nbsp;=&nbsp;6371&nbsp;km, což je [[Koule#Vlastnosti|poloměr koule o stejném objemu]] jako je skutečný [[Země|objem Země]]. S gravitačním zrychlením by tělesa padala k Zemi, kdyby se Země neotáčela.
 Na tělesa otáčející se spolu se Zemí (tedy ve [[Vztažná soustava|vztažné soustavě]] spojené s povrchem Země) působí výslednice dvou sil: gravitační síly a