Multimediaexpo.cz je již 18 let na českém internetu !!
Odstředivá síla
Z Multimediaexpo.cz
Odstředivá (centrifugální) síla (často značená Fo) je jedna ze setrvačných sil (zdánlivá síla), které působí na těleso v otáčející se vztažné soustavě. Závisí na volbě vztažné soustavy. V inerciálních vztažných soustavách žádné odstředivé síly nepůsobí. Důsledkem odstředivé síly je odstředivé zrychlení.
Někdy se však odstředivou silou nazývá reakce (reakční síla podle Třetího Newtonova zákona) vznikající při působení dostředivé síly v inerciální vztažné soustavě. V tomto případě je velikost odstředivé síly stejná jako velikost dostředivé síly. Směr odstředivé síly je od středu křivosti trajektorie tělesa (od středu kružnice). Tato síla ovšem nepůsobí na těleso, na které působí dostředivá síla, jak se často chybně uvádí. Kdyby tomu tak bylo, součet odstředivé a dostředivé síly by byl nulový a těleso by se pohybovalo podle Prvního Newtonova zákona rovnoměrně přímočaře, což je však spor s předpokladem, že se těleso pohybuje křivočaře.
Obsah |
Náklon v zatáčce
Na těleso pohybující se v gravitačním poli v neinerciální vztažné soustavě působí kromě odstředivé (na obrázku Fs) také tíhová síla (FG). Při vhodném úhlu náklonu α se vyrovná odstředivá síla částí tíhové síly (F2). Těleso tak při pohybu zůstává nakloněné, ale nespadne. Příkladem takového pohybu je bruslař, který zatáčí.
Rotace Země
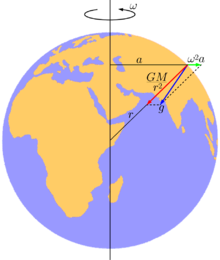
Planeta Země je přibližně koule, která se pomalu otáčí kolem své osy, takže vztažná soustava s ní spjatá není přesně inerciální. (Lze se o tom přesvědčit například Foucaultovým kyvadlem.) V soustavě spjaté se Zemí působí na předměty gravitační síla a zároveň setrvačná odstředivá síla směrem od osy otáčení. Úhlová rychlost \(\omega\) je pro všechny předměty na Zemi stejná (jedna otáčka za den). Setrvačné odstředivé zrychlení tedy roste úměrně poloměru \(r\) kružnice, kterou předmět opisuje, čili jeho vzdálenosti od zemské osy. Tu lze vypočítat jako \(r=R\left|\cos\varphi\right|\), kde \(R\) je poloměr planety a \(\varphi\) je zeměpisná šířka. Odstředivé zrychlení je potom \(a_{\mathrm o} = \omega^2r = \omega^2 R \left|\cos\varphi\right|\). Největší odstředivé zrychlení je na rovníku, nulové na pólech, v Praze má hodnotu zhruba 0,022 m/s². Setrvačná odstředivá síla se vektorově sčítá se silou gravitační a výsledkem je tíhová síla, která nás tlačí k Zemi. Zatímco gravitace míří přesně do středu planety (těžiště), tíhová síla má směr mírně odlišný. Zavěsíme-li na severní polokouli olovnici, nemíří přesně do středu Země, protože je odstředivou silou mírně tažena k jihu. Zároveň je mírně nadlehčována.
YouTube
| The Most Terrifying Rides In The World (HD) |
| American Got Talent S3 Russian Bar Trio (anglicky) |
Související články
Externí odkazy
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |