The final launch of the Allmultimedia.org will take place on February 24, 2026
(shortly after the 2026 Winter Olympics).
Dovolená : 23. prosinec 2025 — 29. prosinec 2025
Holidays : December 23, 2025 — December 29, 2025
Elektronvolt
Z Multimediaexpo.cz
(+ Vylepšení) |
m (Nahrazení textu „</math>“ textem „\)</big>“) |
||
| (Není zobrazena jedna mezilehlá verze.) | |||
| Řádka 14: | Řádka 14: | ||
}}</ref> Používá se běžně k měření malých množství energie zejména v [[Fyzika částic|částicové fyzice]], [[fyzikální chemie|fyzikální chemii]] apod., protože obvyklá energie jedné částice je v [[joule]]ch velmi malé číslo. Zároveň je to jednotka technicky výhodná vzhledem k běžným metodám měření energie částic. | }}</ref> Používá se běžně k měření malých množství energie zejména v [[Fyzika částic|částicové fyzice]], [[fyzikální chemie|fyzikální chemii]] apod., protože obvyklá energie jedné částice je v [[joule]]ch velmi malé číslo. Zároveň je to jednotka technicky výhodná vzhledem k běžným metodám měření energie částic. | ||
Elektronvolt lze převést na odvozenou jednotku energie soustavy SI [[joule]] podle vztahu: | Elektronvolt lze převést na odvozenou jednotku energie soustavy SI [[joule]] podle vztahu: | ||
| - | : < | + | : <big>\(1\,\mathrm{eV} = 1{,}602\,176\,487(40) \times 10^{-19}\,\mathrm{J} \,.\)</big><ref name="CODATA">{{Citace periodika |
| příjmení = Mohr | | příjmení = Mohr | ||
| jméno = Peter J. | | jméno = Peter J. | ||
| Řádka 129: | Řádka 129: | ||
[[Jaderná fúze|Sloučením]] jednoho jádra atomu [[deuterium|deuteria]] s jádrem [[tritium|tritia]] se uvolní 17,6 MeV.<ref name="Nave"/> V [[Obrazovka CRT|CRT obrazovkách]] barevných [[televizor]]ů jsou elektrony urychlovány vysokým napětím kolem 32 tisíc voltů, takže elektrony získávají kinetickou energii 32 keV. Dobře se elektronvolt hodí k měření energie [[chemická vazba|chemických vazeb]], jsou to řádově jednotky či desítky eV na jednu [[molekula|molekulu]].<ref name="Nave"/> K vytržení elektronu z [[atom]]u [[vodík]]u ([[ionizace|ionizaci]]) je potřeba 13,6 eV.<ref name="Nave"/> Řádově jednotky eV má také energie [[foton]]ů viditelného světla.<ref name="Nave"/> Energie menší než elektronvolt se vyskytují v [[termodynamika|termodynamice]], například střední [[kinetická energie]] částic [[vzduch]]u při [[pokojová teplota|pokojové teplotě]] je 38 meV (milielektronvolt).<ref name="Nave"/> | [[Jaderná fúze|Sloučením]] jednoho jádra atomu [[deuterium|deuteria]] s jádrem [[tritium|tritia]] se uvolní 17,6 MeV.<ref name="Nave"/> V [[Obrazovka CRT|CRT obrazovkách]] barevných [[televizor]]ů jsou elektrony urychlovány vysokým napětím kolem 32 tisíc voltů, takže elektrony získávají kinetickou energii 32 keV. Dobře se elektronvolt hodí k měření energie [[chemická vazba|chemických vazeb]], jsou to řádově jednotky či desítky eV na jednu [[molekula|molekulu]].<ref name="Nave"/> K vytržení elektronu z [[atom]]u [[vodík]]u ([[ionizace|ionizaci]]) je potřeba 13,6 eV.<ref name="Nave"/> Řádově jednotky eV má také energie [[foton]]ů viditelného světla.<ref name="Nave"/> Energie menší než elektronvolt se vyskytují v [[termodynamika|termodynamice]], například střední [[kinetická energie]] částic [[vzduch]]u při [[pokojová teplota|pokojové teplotě]] je 38 meV (milielektronvolt).<ref name="Nave"/> | ||
Rychlost elektronu s kinetickou energií 1 eV je přibližně 593 km/s. Rychlost protonu se stejnou kinetickou energií je pak jen 13,8 km/s. | Rychlost elektronu s kinetickou energií 1 eV je přibližně 593 km/s. Rychlost protonu se stejnou kinetickou energií je pak jen 13,8 km/s. | ||
| - | Velikost elektronvoltu v jednotkách SI se určuje měřením náboje elektronu. Nejpřesnější ze známých metod je měření [[Josephsonův jev|Josephsonova jevu]], kterým se určí hodnota Josephsonovy konstanty < | + | Velikost elektronvoltu v jednotkách SI se určuje měřením náboje elektronu. Nejpřesnější ze známých metod je měření [[Josephsonův jev|Josephsonova jevu]], kterým se určí hodnota Josephsonovy konstanty <big>\(K_{\mathrm J}\)</big>. Velikost elementárního náboje se pak stanoví ze vztahu <big>\(e = 2/\left(R_{\mathrm K} K_{\mathrm J}\right)\)</big>. Zde <big>\(R_{\mathrm K}\)</big> je [[kvantový Hallův jev#von Klitzingova konstanta|von Klitzingova konstanta]], která je změřena řádově přesněji než <big>\(K_{\mathrm J}\)</big>. Relativní [[směrodatná odchylka]] měření Josephsonovy konstanty je 2,5×10<sup>-8</sup> (2,5 miliontiny [[procento|procenta]]) a právě takovou přesnost má i převod elektronvoltu na jouly.<ref name="CODATA"/> |
== Užití při měření == | == Užití při měření == | ||
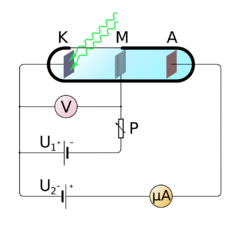
[[Soubor:Photoeffect.png|thumb|240px|Zařízení k měření fotoelektrického jevu: K – [[katoda]], M – mřížka, A – [[anoda]], P – [[potenciometr]]]] | [[Soubor:Photoeffect.png|thumb|240px|Zařízení k měření fotoelektrického jevu: K – [[katoda]], M – mřížka, A – [[anoda]], P – [[potenciometr]]]] | ||
| Řádka 143: | Řádka 143: | ||
|- | |- | ||
|[[Planckova konstanta]] | |[[Planckova konstanta]] | ||
| - | |< | + | |<big>\(h=4{,}135\,667\,33(10) \times 10^{-15}\,\mathrm{eV \cdot s}\)</big> |
|Elementární [[kvantová mechanika|kvantum]] [[akce (fyzika)|akce]] | |Elementární [[kvantová mechanika|kvantum]] [[akce (fyzika)|akce]] | ||
|- | |- | ||
|redukovaná Planckova konstanta | |redukovaná Planckova konstanta | ||
| - | |< | + | |<big>\(\hbar=6{,}582\,118\,99(16) \times 10^{-16}\,\mathrm{eV \cdot s}\)</big> |
| - | |< | + | |<big>\(\hbar=h/2\pi\,,\)</big> elementární kvantum [[moment hybnosti|momentu hybnosti]] |
|- | |- | ||
|[[Boltzmannova konstanta]] | |[[Boltzmannova konstanta]] | ||
| - | |< | + | |<big>\(k=8{,}617\,343(15) \times 10^{-5}\,\mathrm{eV/K}\)</big> |
|Vztah mezi energií částic a [[termodynamická teplota|teplotou]] [[Termodynamický systém|termodynamického systému]] | |Vztah mezi energií částic a [[termodynamická teplota|teplotou]] [[Termodynamický systém|termodynamického systému]] | ||
|- | |- | ||
|[[Rydbergova konstanta]] | |[[Rydbergova konstanta]] | ||
| - | |< | + | |<big>\(R_\infty hc=13{,}605\,691\,93(34)\,\mathrm{eV}\)</big> |
|[[ionizace|Ionizační]] energie [[vodík]]u | |[[ionizace|Ionizační]] energie [[vodík]]u | ||
|- | |- | ||
|[[Atomová hmotnostní konstanta]] | |[[Atomová hmotnostní konstanta]] | ||
| - | |< | + | |<big>\(m_{\mathrm u}c^2=931{,}494\,028(23)\,\mathrm{MeV}\)</big> |
| - | | Dvanáctina klidové energie atomu [[uhlík]]u < | + | | Dvanáctina klidové energie atomu [[uhlík]]u <big>\({}^{12}_{ 6}\mbox{C}\)</big> |
|- | |- | ||
|[[Planckova energie]] | |[[Planckova energie]] | ||
| - | |< | + | |<big>\(E_{\mathrm P}=1{,}220\,892(61) \times 10^{19}\,\mathrm{GeV}\)</big> |
|[[Přirozená soustava jednotek|Přirozená jednotka]] energie | |[[Přirozená soustava jednotek|Přirozená jednotka]] energie | ||
|- | |- | ||
|[[Bohrův magneton]] | |[[Bohrův magneton]] | ||
| - | |< | + | |<big>\(\mu_{\mathrm B}=5{,}788\,381\,7555(79) \times 10^{-5}\,\mathrm{eV/T}\)</big> |
|Jednotka pro [[magnetický moment]] elektronu | |Jednotka pro [[magnetický moment]] elektronu | ||
|- | |- | ||
|[[Jaderný magneton]] | |[[Jaderný magneton]] | ||
| - | |< | + | |<big>\(\mu_{\mathrm N}=3{,}152\,451\,2326(45) \times 10^{-8}\,\mathrm{eV/T}\)</big> |
|Jednotka pro magnetický moment [[atomové jádro|atomových jader]] | |Jednotka pro magnetický moment [[atomové jádro|atomových jader]] | ||
|- | |- | ||
| Řádka 178: | Řádka 178: | ||
[[Soubor:Colors in eV.png|thumb|260px|Barva světla přímo souvisí s energií fotonu. [[Lidské oko]] vnímá rozsah 1,65÷3,27 eV.]] | [[Soubor:Colors in eV.png|thumb|260px|Barva světla přímo souvisí s energií fotonu. [[Lidské oko]] vnímá rozsah 1,65÷3,27 eV.]] | ||
Podle [[kvantová teorie|kvantové teorie]] se [[světlo]] a veškeré jiné [[elektromagnetické záření]] skládá z [[částicová fyzika|částic]] – [[foton]]ů, jejichž energie je přímo úměrná frekvenci světla. | Podle [[kvantová teorie|kvantové teorie]] se [[světlo]] a veškeré jiné [[elektromagnetické záření]] skládá z [[částicová fyzika|částic]] – [[foton]]ů, jejichž energie je přímo úměrná frekvenci světla. | ||
| - | : < | + | : <big>\(E=hf={hc\over\lambda}\)</big> |
| - | Zde < | + | Zde <big>\(h\)</big> je Planckova konstanta, <big>\(c\)</big> je [[rychlost světla]] ve [[vakuum|vakuu]], <big>\(f\)</big> je [[frekvence]] a <big>\(\lambda\)</big> je [[vlnová délka]]. Vyjádříme-li součin <big>\(hc\)</big> v jednotkách eV <big>\(\cdot\)</big> nm, dostaneme užitečné vyjádření energie fotonu v elektronvoltech. |
| - | : < | + | : <big>\(E={1239{,}841\,875(31)\,\mathrm{eV \cdot nm}\over\lambda} \;\dot=\; {1240\,\mathrm{nm}\over\lambda}\,\mathrm{eV}\)</big><ref group="pozn" name="hc">Uvedená hodnota <big>\(hc\)</big> vznikla vynásobením hodnoty <big>\(\hbar c\)</big> dle CODATA 2006 konstantou <big>\(2\pi\)</big> kvůli přepočtu <big>\(\hbar\)</big> na <big>\(h\)</big>.</ref> |
Viditelné světlo i okolní [[infračervené záření|infračervené]] a [[ultrafialové záření|ultrafialové]] záření je tedy tvořeno fotony s energií řádově v jednotkách elektronvoltů. | Viditelné světlo i okolní [[infračervené záření|infračervené]] a [[ultrafialové záření|ultrafialové]] záření je tedy tvořeno fotony s energií řádově v jednotkách elektronvoltů. | ||
== Další veličiny udávané v elektronvoltech == | == Další veličiny udávané v elektronvoltech == | ||
| - | V částicové fyzice se elektronvolty, jejich násobky a mocniny běžně užívají i k vyjádření hodnot jiných veličin než energie. Tato konvence je postavena na faktu, že veličiny k sobě pojí základní fyzikální vztah, který má tvar [[přímá úměrnost|přímé úměrnosti]]. Je-li energie < | + | V částicové fyzice se elektronvolty, jejich násobky a mocniny běžně užívají i k vyjádření hodnot jiných veličin než energie. Tato konvence je postavena na faktu, že veličiny k sobě pojí základní fyzikální vztah, který má tvar [[přímá úměrnost|přímé úměrnosti]]. Je-li energie <big>\(E\)</big> v nějakém kontextu úměrná veličině <big>\(A\)</big>, zapisujeme to jako rovnici |
| - | : < | + | : <big>\(E=f A\,,\)</big> |
| - | kde < | + | kde <big>\(f\)</big> je konstanta úměrnosti. Obvykle je <big>\(f\)</big> některá ze základních fyzikálních konstant, nejčastěji [[rychlost světla]] ve vakuu <big>\(c\)</big>, redukovaná [[Planckova konstanta]] <big>\(\hbar\)</big>, [[Boltzmannova konstanta]] <big>\(k\)</big>, [[gravitační konstanta]] <big>\(G\)</big>, případně jejich kombinace. Konstanta určuje způsob přepočtu veličiny <big>\(A\)</big> na energii a také zpět: |
| - | : < | + | : <big>\(A=E/f \,.\)</big> |
| - | Jako jednotku pro veličinu < | + | Jako jednotku pro veličinu <big>\(A\)</big> můžeme na základě tohoto vztahu použít jednotku energie vydělenou konstantou <big>\(f\)</big>. Za jednotku energie se obvykle volí elektronvolt, takže jednotku zapisujeme takto: |
| - | : < | + | : <big>\([A]=\mathrm{eV}/f \,.\)</big> |
| - | Tento zápis kóduje způsob, jak hodnotu veličiny převést na jiné jednotky. Například klidová hmotnost protonu může být uvedena jako < | + | Tento zápis kóduje způsob, jak hodnotu veličiny převést na jiné jednotky. Například klidová hmotnost protonu může být uvedena jako <big>\(m_\mathrm{p} = 938\,\mathrm{MeV}/c^2\)</big>. Chceme-li hodnotu převést na základní jednotku SI – kilogram, je třeba přepočítat <big>\(938 \times 10^6\,\mathrm{eV}\)</big> na jouly a výsledek podělit druhou [[mocnina|mocninou]] rychlosti světla <big>\(c \;\dot=\; 3 \times 10^8\, \mathrm{m/s}\)</big>. Číselně tedy provádíme tento výpočet: |
| - | : < | + | : <big>\(\{m\} = 938 \times 10^6 {1{,}602 \times 10^{-19} \over \left( 3 \times 10^8 \right)^2} = 1{,}67 \times 10^{-27}\)</big> |
| - | Hmotnost protonu je tedy přibližně < | + | Hmotnost protonu je tedy přibližně <big>\(1{,}67\times10^{-27}\,\mathrm{kg}\)</big>. |
| - | Uvedený zápis je konzistentní a umožňuje hodnoty kdykoli přepočítat na jiné jednotky a to i čtenáři, který nezná příslušný fyzikální vztah. Částicoví fyzikové tuto konvenci znají a používají ke zjednodušení některých výpočtů. Někdy přitom ale vynechávají konstanty, takže například hmotnost protonu může být uvedena jako < | + | Uvedený zápis je konzistentní a umožňuje hodnoty kdykoli přepočítat na jiné jednotky a to i čtenáři, který nezná příslušný fyzikální vztah. Částicoví fyzikové tuto konvenci znají a používají ke zjednodušení některých výpočtů. Někdy přitom ale vynechávají konstanty, takže například hmotnost protonu může být uvedena jako <big>\(m_\mathrm{p} = 938\,\mathrm{MeV}\)</big>. V jednotkách SI je to zápis formálně nesprávný a pro neznalého člověka může být matoucí, protože zakrývá způsob převodu jednotek. V publikaci užívající tento zápis bývá ve zvláštní sekci uvedeno, že ve výpočtech používá místo SI některou tzv. [[přirozená soustava jednotek|přirozenou soustavu jednotek]]. Jednotky jsou v tom případě zavedeny tak, aby základní konstanty měly číselnou hodnotu 1. Je-li například <big>\({c}=1\)</big>, pak tato konstanta odpadá i ze zápisu jednotek: <big>\(\mathrm{eV}/c^2=\mathrm{eV}\)</big>. Dle této konvence je možné uvádět v elektronvoltech, jejich násobcích a mocninách dokonce ''všechny'' veličiny relevantní pro daný text.<ref>{{Citace elektronické monografie |
| příjmení = Staroba | | příjmení = Staroba | ||
| jméno = Pavel | | jméno = Pavel | ||
| Řádka 207: | Řádka 207: | ||
Níže uvádíme příklady veličin, k jejichž vyjádření se používají elektronvolty v kombinaci s určitou konstantou, a kontext, který vedl k volbě převodního vztahu. | Níže uvádíme příklady veličin, k jejichž vyjádření se používají elektronvolty v kombinaci s určitou konstantou, a kontext, který vedl k volbě převodního vztahu. | ||
=== Hmotnost === | === Hmotnost === | ||
| - | [[Soubor:CGKilogram.jpg|thumb|240px|Mezinárodní prototyp [[kilogram]]u má hmotnost cca < | + | [[Soubor:CGKilogram.jpg|thumb|240px|Mezinárodní prototyp [[kilogram]]u má hmotnost cca <big>\(5{,}61\times 10^{35}\,\mathrm{eV}/c^2\)</big>.]] |
| - | Podle [[Albert Einstein|Einsteinovy]] [[teorie relativity]] odpovídá každé [[hmotnost]]i určité množství energie podle vztahu [[E=mc²]], kde < | + | Podle [[Albert Einstein|Einsteinovy]] [[teorie relativity]] odpovídá každé [[hmotnost]]i určité množství energie podle vztahu [[E=mc²]], kde <big>\(c\)</big> je konstanta ([[rychlost světla]] ve vakuu). Jde o vztah přímé úměrnosti, což umožňuje měřit hmotnost ve stejných jednotkách jako energii. Například klidovou hmotnost elektronu <big>\(m_\mathrm{e}=9{,}11 \times 10^{-31}\,\mathrm{kg}\)</big> můžeme vynásobit <big>\(c^2\)</big>, čímž obdržíme klidovou energii v joulech. Po převodu na elektronvolty můžeme psát <big>\(m_\mathrm{e} = 511\,\mathrm{keV}/c^2\)</big>, což se běžně zkráceně zapisuje i jako <big>\(m_\mathrm{e}=511\,\mathrm{keV}\)</big>. Tato hodnota odpovídá energii uvolněné při [[anihilace|anihilaci]] elektronu. |
| - | : < | + | : <big>\(1\,\mathrm{eV}/c^2 = {1{,}602\,176\,487(40) \times 10^{-19} \,\mathrm{J} \over \left(299\,792\,458\,\mathrm{m/s} \right)^2} = 1{,}782\,661\,758(45) \times 10^{-36}\,\mathrm{kg}\)</big> |
| - | Ve fyzice [[elementární částice|elementárních částic]] se klidová hmotnost udává běžně v jednotkách < | + | Ve fyzice [[elementární částice|elementárních částic]] se klidová hmotnost udává běžně v jednotkách <big>\(\mathrm{MeV}/c^2\)</big>, což odpovídá přibližně <big>\(1{,}782\,662 \times 10^{-30}\,\mathrm{kg}\)</big> (tj. zhruba dvojnásobek hmotnosti elektronu). |
=== Hybnost === | === Hybnost === | ||
[[Hybnost]] fotonu je přímo úměrná jeho energii, přičemž konstantou úměrnosti je rychlost světla ve vakuu. | [[Hybnost]] fotonu je přímo úměrná jeho energii, přičemž konstantou úměrnosti je rychlost světla ve vakuu. | ||
| - | : < | + | : <big>\(p={E\over c}\)</big> |
| - | Dle tohoto vztahu můžeme přirozeně měřit hybnost v jednotkách < | + | Dle tohoto vztahu můžeme přirozeně měřit hybnost v jednotkách <big>\(\mathrm{eV}/c\)</big>. |
| - | : < | + | : <big>\(1\,\mathrm{eV/c} = {1{,}602\,176\,487(40) \times 10^{-19}\,\mathrm{J} \over 299\,792\,458\,\mathrm{m/s} } = 5{,}344\,285\,50(13) \times 10^{-28}\,\mathrm{kg \cdot m \cdot s^{-1}}\)</big> |
Hybnost fotonu má v těchto jednotkách číselně stejnou hodnotu jako jeho energie. | Hybnost fotonu má v těchto jednotkách číselně stejnou hodnotu jako jeho energie. | ||
| - | Výhodnost těchto jednotek lze demonstrovat na příkladu, kdy máme určit hybnost elektronu, který byl urychlen elektrickým napětím < | + | Výhodnost těchto jednotek lze demonstrovat na příkladu, kdy máme určit hybnost elektronu, který byl urychlen elektrickým napětím <big>\(150\,\mathrm{kV}\)</big>. Podle definice elektronvoltu získal elektron kinetickou energii <big>\(E_{\mathrm{k}}=150\,\mathrm{keV}\)</big>. Klidová hmotnost elektronu je <big>\(m_{\mathrm{e}}=511\,\mathrm{keV}/c^2\)</big>, takže jeho energie v klidu je <big>\(E_0=m_{\mathrm{e}} c^2 = 511\,\mathrm{keV}\)</big>. Celková energie urychlené částice je tedy jednoduše <big>\(E = E_0 + E_{\mathrm{k}} = 661\,\mathrm{keV}\)</big>. K výpočtu hybnosti použijeme [[speciální teorie relativity|relativistický]] vztah známý jako [[Pythagorova věta o energii]]: |
| - | : < | + | : <big>\(E^2=E_0^2+\left(pc\right)^2 \,.\)</big> |
Odtud plyne | Odtud plyne | ||
| - | : < | + | : <big>\(pc = \sqrt{E^2-E_0^2} = \sqrt{661^2-511^2} \,\mathrm{keV} \;\dot=\; 419 \,\mathrm{keV}\)</big>. |
| - | Hybnost tedy můžeme zapsat jako < | + | Hybnost tedy můžeme zapsat jako <big>\(p=419 \,\mathrm{keV}/c\)</big>. Je vidět, že konstanta <big>\(c\)</big> se ve vztazích chová tak, že ani není třeba znát její hodnotu a číselné operace jsou jednoduché. |
=== Termodynamická teplota === | === Termodynamická teplota === | ||
[[Soubor:Temperature in eV.png|thumb|200px|Teplota lidského těla je 26,7 meV/''k''.]] | [[Soubor:Temperature in eV.png|thumb|200px|Teplota lidského těla je 26,7 meV/''k''.]] | ||
| - | [[Termodynamická teplota]] se místo [[kelvin]]ů někdy udává v elektronvoltech. Převod je dán hodnotou [[Boltzmannova konstanta|Boltzmannovy konstanty]] < | + | [[Termodynamická teplota]] se místo [[kelvin]]ů někdy udává v elektronvoltech. Převod je dán hodnotou [[Boltzmannova konstanta|Boltzmannovy konstanty]] <big>\(k\)</big>. |
| - | : < | + | : <big>\(1\mathrm{eV}/k = {1\mathrm{eV} \over 8{,}617\,343(15) \times 10^{-5}\,\mathrm{eV/K}} = 11\,604{,}505(20)\,\mathrm{K}\)</big> |
Například teplotu v jádru [[Slunce]] 15,7 milionu kelvinů<ref>{{Citace elektronické monografie | Například teplotu v jádru [[Slunce]] 15,7 milionu kelvinů<ref>{{Citace elektronické monografie | ||
| příjmení = Williams | | příjmení = Williams | ||
| Řádka 237: | Řádka 237: | ||
| datum přístupu = 2009-08-02 | | datum přístupu = 2009-08-02 | ||
| jazyk = anglicky | | jazyk = anglicky | ||
| - | }}</ref> lze zapsat jako < | + | }}</ref> lze zapsat jako <big>\(1\,350\,\mathrm{eV}/k\)</big>. V tomto smyslu je povrchová teplota Slunce přibližně <big>\(0{,}5\,\mathrm{eV}/k\)</big>. Po vynásobení faktorem <big>\({3\over 2} k\)</big> získáme střední [[kinetická energie|kinetickou energii]] částic fotosféry <big>\(0{,}75\,\mathrm{eV}\)</big>.<ref group = "pozn">Z historických a praktických důvodů není faktor ve vztahu mezi kinetickou energií a teplotou <big>\(E_{\mathrm k} = 3/2\ kT\)</big> roven jedné. Vymizí tak číselné konstanty v jiných vztazích, jako je např. [[stavová rovnice]] ideálního plynu, [[Boltzmannův faktor]] či [[Planckův vyzařovací zákon]].</ref> |
=== Časy a vzdálenosti === | === Časy a vzdálenosti === | ||
| - | U částic s velmi krátkou [[střední doba života|střední dobou života]] < | + | U částic s velmi krátkou [[střední doba života|střední dobou života]] <big>\(\tau\)</big> se místo ní někdy udává tzv. [[rozpadová šířka]], která má rozměr energie. |
| - | : < | + | : <big>\(\Gamma = {\hbar\over\tau}\)</big> |
| - | Například [[mezon]] < | + | Například [[mezon]] <big>\(\mathrm{B^0}\)</big> má dobu života asi 1,53 pikosekund,<ref>{{Citace elektronické monografie |
| příjmení = Vankov | | příjmení = Vankov | ||
| jméno = Peter Hristoforov | | jméno = Peter Hristoforov | ||
| Řádka 253: | Řádka 253: | ||
| místo = | | místo = | ||
| jazyk = anglicky | | jazyk = anglicky | ||
| - | }}</ref> čemuž odpovídá rozpadová šířka < | + | }}</ref> čemuž odpovídá rozpadová šířka <big>\(4{,}30 \times 10^{-4}\,\mathrm{eV}\)</big>. Je vidět, že časové údaje lze udávat v jednotkách <big>\(\mathrm{eV^{-1}}\)</big>, či přesněji řečeno <big>\(\mathrm{eV^{-1}}\hbar\)</big>. |
| - | : < | + | : <big>\(1\,\mathrm{eV^{-1}} \hbar = 6{,}582\,118\,99(16) \times 10^{-16} \,\mathrm{s}\)</big> |
| - | A protože rychlost světla ve vakuu dává přímý přepočet mezi jednotkami [[čas]]u a [[vzdálenost]]i, je možné měřit i vzdálenost v jednotkách < | + | A protože rychlost světla ve vakuu dává přímý přepočet mezi jednotkami [[čas]]u a [[vzdálenost]]i, je možné měřit i vzdálenost v jednotkách <big>\(\mathrm{eV^{-1}}\)</big>, či přesněji zapsáno <big>\(\mathrm{eV^{-1}} \hbar c\)</big>. |
| - | : < | + | : <big>\(1\,\mathrm{eV^{-1}} \hbar c = 1{,}973\,269\,631(49) \times 10^{-7} \,\mathrm{m}\)</big><ref name="CODATA"/> |
Vzhledem k typickým malým vzdálenostem ve světě částic, používá se tento vztah často ve tvarech<ref name="PDG">{{Citace periodika | Vzhledem k typickým malým vzdálenostem ve světě částic, používá se tento vztah často ve tvarech<ref name="PDG">{{Citace periodika | ||
| příjmení = Amsler | | příjmení = Amsler | ||
| Řádka 280: | Řádka 280: | ||
| jazyk = anglicky | | jazyk = anglicky | ||
}}</ref>: | }}</ref>: | ||
| - | : < | + | : <big>\(1\,\mathrm{eV^{-1}} \hbar c = 197{,}326\,9631(49) \,\mathrm{nm} \,,\)</big> |
| - | : < | + | : <big>\(1\,\mathrm{MeV^{-1}} \hbar c = 197{,}326\,9631(49) \,\mathrm{fm} \,.\)</big> |
== Historie == | == Historie == | ||
Poprvé byla jednotka elektronvolt, tehdy ještě pod názvem „ekvivalent voltu“, použita roku [[1912]] v časopisu Philosophical Magazine v článku Karla Taylora Comptona a Owena Willanse Richardsona „{{cizojazyčně|en|The Photoelectric Effect}}“ o [[fotoelektrický jev|fotoelektrickém jevu]].<ref name="madore1">{{Citace elektronické monografie | Poprvé byla jednotka elektronvolt, tehdy ještě pod názvem „ekvivalent voltu“, použita roku [[1912]] v časopisu Philosophical Magazine v článku Karla Taylora Comptona a Owena Willanse Richardsona „{{cizojazyčně|en|The Photoelectric Effect}}“ o [[fotoelektrický jev|fotoelektrickém jevu]].<ref name="madore1">{{Citace elektronické monografie | ||
Aktuální verze z 14. 8. 2022, 14:51
Elektronvolt (značka eV) je jednotka práce a energie mimo soustavu SI. Odpovídá kinetické energii, kterou získá elektron urychlený ve vakuu napětím jednoho voltu.[1] Používá se běžně k měření malých množství energie zejména v částicové fyzice, fyzikální chemii apod., protože obvyklá energie jedné částice je v joulech velmi malé číslo. Zároveň je to jednotka technicky výhodná vzhledem k běžným metodám měření energie částic. Elektronvolt lze převést na odvozenou jednotku energie soustavy SI joule podle vztahu:
Hodnota číselně odpovídá náboji elektronu v coulombech, protože práce vykonaná na náboji elektrickou silou se počítá jako součin náboje (1 e) a napětí (1 V). Stejnou energii získá při pohybu v elektrostatickém poli i jiná částice se stejně velkým nábojem, například proton či mion. Elektronvolt není mezi standardními jednotkami soustavy SI. Jeho hodnota je určována experimentálně a postupně se upřesňuje.[3] Přesto Mezinárodní výbor pro míry a váhy povoluje elektronvolt k užívání společně s ostatními jednotkami SI,[4] jakož i další dvě experimentálně stanovené jednotky: atomovou hmotnostní konstantu a astronomickou jednotku. Elektronvolt se běžně využívá pro vyjádření mnoha dalších veličin, například hmotnosti, teploty nebo dokonce času.
Obsah |
Velikost jednotky
Elektronvolt je v běžných měřítkách extrémně malé množství energie. Energie pohybu letícího komára je přibližně bilion elektronvoltů.[5] Jednotka je proto užitečná tam, kde jsou typické energie velmi malé, to znamená ve světě částic. Také zde je 1 eV často poměrně malá energie, takže se používají větší násobky a předpony: 1 keV je tisíc eV, 1 MeV je milion eV, 1 GeV je miliarda eV, 1 TeV je bilion eV. Někdy se zkratka používá jako akronym, lze se tedy setkat i s jejím skloňováním.[6] Největší urychlovač částic (LHC) dodá každému protonu energii 7 TeV.[7] Rozbitím jediného jádra uranu 235U se uvolní přibližně 215 MeV.[8] Sloučením jednoho jádra atomu deuteria s jádrem tritia se uvolní 17,6 MeV.[8] V CRT obrazovkách barevných televizorů jsou elektrony urychlovány vysokým napětím kolem 32 tisíc voltů, takže elektrony získávají kinetickou energii 32 keV. Dobře se elektronvolt hodí k měření energie chemických vazeb, jsou to řádově jednotky či desítky eV na jednu molekulu.[8] K vytržení elektronu z atomu vodíku (ionizaci) je potřeba 13,6 eV.[8] Řádově jednotky eV má také energie fotonů viditelného světla.[8] Energie menší než elektronvolt se vyskytují v termodynamice, například střední kinetická energie částic vzduchu při pokojové teplotě je 38 meV (milielektronvolt).[8] Rychlost elektronu s kinetickou energií 1 eV je přibližně 593 km/s. Rychlost protonu se stejnou kinetickou energií je pak jen 13,8 km/s. Velikost elektronvoltu v jednotkách SI se určuje měřením náboje elektronu. Nejpřesnější ze známých metod je měření Josephsonova jevu, kterým se určí hodnota Josephsonovy konstanty \(K_{\mathrm J}\). Velikost elementárního náboje se pak stanoví ze vztahu \(e = 2/\left(R_{\mathrm K} K_{\mathrm J}\right)\). Zde \(R_{\mathrm K}\) je von Klitzingova konstanta, která je změřena řádově přesněji než \(K_{\mathrm J}\). Relativní směrodatná odchylka měření Josephsonovy konstanty je 2,5×10-8 (2,5 miliontiny procenta) a právě takovou přesnost má i převod elektronvoltu na jouly.[2]
Užití při měření
V technické praxi je výhodné, že pro částice s elementárním nábojem odpovídá změna energie v elektronvoltech přímo elektrickému napětí ve voltech, kterým je částice urychlena (či zbrzděna). Příkladem může být aparatura k pozorování vnějšího fotoelektrického jevu, kde se užívá brzdné elektrické pole ke zjištění energie elektronů. Světlo (či jiné záření) prochází okénkem do evakuované baňky a dopadá na katodu, aby z jejího povrchu vytrhlo elektrony. Ty prolétají skrze mřížku, dopadají na anodu a vytvářejí tak v obvodu elektrický proud, který měříme mikroampérmetrem. Abychom stanovili energii vyletujících elektronů, nastavíme pomocí potenciometru brzdné napětí mezi katodu a mřížku. Málo energetické elektrony jsou tímto elektrickým polem vráceny zpět na katodu a neúčastní se vedení proudu. Pokud má ale elektron dostatečnou kinetickou energii, brzdné pole překoná a pokračuje k anodě. Potřebná kinetická energie v elektronvoltech přímo odpovídá brzdnému napětí ve voltech. Můžeme tedy experimentálně zjistit krajní hodnotu napětí mezi katodou a mřížkou, při němž obvodem ještě prochází proud, například 1,2 voltu. Znamená to, že světlo dodává elektronům kinetickou energii 1,2 elektronvoltu. V praxi tedy často porovnáváme neznámou hodnotu energie částice přímo s elektronvoltem a nikoli s jednotkami soustavy SI. Je to jeden z hlavních důvodů k zavedení této jednotky. Nepřesnost převodního koeficientu mezi eV a J je obvykle zcela zanedbatelná vzhledem k chybám měření v běžných laboratorních podmínkách. Navíc elektronvolt lze podle jeho definice realizovat výrazně přesněji než joule podle definice SI.
Konstanty
Některé fyzikální konstanty mají rozměr energie, případně v kombinaci s dalšími veličinami. K jejich vyjádření lze místo joulů používat elektronvolty. Skupina CODATA uvádí v doporučení z roku 2006 tyto hodnoty konstant a směrodatných odchylek.[2][pozn 2]
| Veličina | Hodnota | Význam |
|---|---|---|
| Planckova konstanta | \(h=4{,}135\,667\,33(10) \times 10^{-15}\,\mathrm{eV \cdot s}\) | Elementární kvantum akce |
| redukovaná Planckova konstanta | \(\hbar=6{,}582\,118\,99(16) \times 10^{-16}\,\mathrm{eV \cdot s}\) | \(\hbar=h/2\pi\,,\) elementární kvantum momentu hybnosti |
| Boltzmannova konstanta | \(k=8{,}617\,343(15) \times 10^{-5}\,\mathrm{eV/K}\) | Vztah mezi energií částic a teplotou termodynamického systému |
| Rydbergova konstanta | \(R_\infty hc=13{,}605\,691\,93(34)\,\mathrm{eV}\) | Ionizační energie vodíku |
| Atomová hmotnostní konstanta | \(m_{\mathrm u}c^2=931{,}494\,028(23)\,\mathrm{MeV}\) | Dvanáctina klidové energie atomu uhlíku \({}^{12}_{ 6}\mbox{C}\) |
| Planckova energie | \(E_{\mathrm P}=1{,}220\,892(61) \times 10^{19}\,\mathrm{GeV}\) | Přirozená jednotka energie |
| Bohrův magneton | \(\mu_{\mathrm B}=5{,}788\,381\,7555(79) \times 10^{-5}\,\mathrm{eV/T}\) | Jednotka pro magnetický moment elektronu |
| Jaderný magneton | \(\mu_{\mathrm N}=3{,}152\,451\,2326(45) \times 10^{-8}\,\mathrm{eV/T}\) | Jednotka pro magnetický moment atomových jader |
Energie fotonů
Podle kvantové teorie se světlo a veškeré jiné elektromagnetické záření skládá z částic – fotonů, jejichž energie je přímo úměrná frekvenci světla.
- \(E=hf={hc\over\lambda}\)
Zde \(h\) je Planckova konstanta, \(c\) je rychlost světla ve vakuu, \(f\) je frekvence a \(\lambda\) je vlnová délka. Vyjádříme-li součin \(hc\) v jednotkách eV \(\cdot\) nm, dostaneme užitečné vyjádření energie fotonu v elektronvoltech.
- \(E={1239{,}841\,875(31)\,\mathrm{eV \cdot nm}\over\lambda} \;\dot=\; {1240\,\mathrm{nm}\over\lambda}\,\mathrm{eV}\)[pozn 3]
Viditelné světlo i okolní infračervené a ultrafialové záření je tedy tvořeno fotony s energií řádově v jednotkách elektronvoltů.
Další veličiny udávané v elektronvoltech
V částicové fyzice se elektronvolty, jejich násobky a mocniny běžně užívají i k vyjádření hodnot jiných veličin než energie. Tato konvence je postavena na faktu, že veličiny k sobě pojí základní fyzikální vztah, který má tvar přímé úměrnosti. Je-li energie \(E\) v nějakém kontextu úměrná veličině \(A\), zapisujeme to jako rovnici
- \(E=f A\,,\)
kde \(f\) je konstanta úměrnosti. Obvykle je \(f\) některá ze základních fyzikálních konstant, nejčastěji rychlost světla ve vakuu \(c\), redukovaná Planckova konstanta \(\hbar\), Boltzmannova konstanta \(k\), gravitační konstanta \(G\), případně jejich kombinace. Konstanta určuje způsob přepočtu veličiny \(A\) na energii a také zpět:
- \(A=E/f \,.\)
Jako jednotku pro veličinu \(A\) můžeme na základě tohoto vztahu použít jednotku energie vydělenou konstantou \(f\). Za jednotku energie se obvykle volí elektronvolt, takže jednotku zapisujeme takto:
- \([A]=\mathrm{eV}/f \,.\)
Tento zápis kóduje způsob, jak hodnotu veličiny převést na jiné jednotky. Například klidová hmotnost protonu může být uvedena jako \(m_\mathrm{p} = 938\,\mathrm{MeV}/c^2\). Chceme-li hodnotu převést na základní jednotku SI – kilogram, je třeba přepočítat \(938 \times 10^6\,\mathrm{eV}\) na jouly a výsledek podělit druhou mocninou rychlosti světla \(c \;\dot=\; 3 \times 10^8\, \mathrm{m/s}\). Číselně tedy provádíme tento výpočet:
- \(\{m\} = 938 \times 10^6 {1{,}602 \times 10^{-19} \over \left( 3 \times 10^8 \right)^2} = 1{,}67 \times 10^{-27}\)
Hmotnost protonu je tedy přibližně \(1{,}67\times10^{-27}\,\mathrm{kg}\). Uvedený zápis je konzistentní a umožňuje hodnoty kdykoli přepočítat na jiné jednotky a to i čtenáři, který nezná příslušný fyzikální vztah. Částicoví fyzikové tuto konvenci znají a používají ke zjednodušení některých výpočtů. Někdy přitom ale vynechávají konstanty, takže například hmotnost protonu může být uvedena jako \(m_\mathrm{p} = 938\,\mathrm{MeV}\). V jednotkách SI je to zápis formálně nesprávný a pro neznalého člověka může být matoucí, protože zakrývá způsob převodu jednotek. V publikaci užívající tento zápis bývá ve zvláštní sekci uvedeno, že ve výpočtech používá místo SI některou tzv. přirozenou soustavu jednotek. Jednotky jsou v tom případě zavedeny tak, aby základní konstanty měly číselnou hodnotu 1. Je-li například \({c}=1\), pak tato konstanta odpadá i ze zápisu jednotek: \(\mathrm{eV}/c^2=\mathrm{eV}\). Dle této konvence je možné uvádět v elektronvoltech, jejich násobcích a mocninách dokonce všechny veličiny relevantní pro daný text.[9] Níže uvádíme příklady veličin, k jejichž vyjádření se používají elektronvolty v kombinaci s určitou konstantou, a kontext, který vedl k volbě převodního vztahu.
Hmotnost

Podle Einsteinovy teorie relativity odpovídá každé hmotnosti určité množství energie podle vztahu E=mc², kde \(c\) je konstanta (rychlost světla ve vakuu). Jde o vztah přímé úměrnosti, což umožňuje měřit hmotnost ve stejných jednotkách jako energii. Například klidovou hmotnost elektronu \(m_\mathrm{e}=9{,}11 \times 10^{-31}\,\mathrm{kg}\) můžeme vynásobit \(c^2\), čímž obdržíme klidovou energii v joulech. Po převodu na elektronvolty můžeme psát \(m_\mathrm{e} = 511\,\mathrm{keV}/c^2\), což se běžně zkráceně zapisuje i jako \(m_\mathrm{e}=511\,\mathrm{keV}\). Tato hodnota odpovídá energii uvolněné při anihilaci elektronu.
- \(1\,\mathrm{eV}/c^2 = {1{,}602\,176\,487(40) \times 10^{-19} \,\mathrm{J} \over \left(299\,792\,458\,\mathrm{m/s} \right)^2} = 1{,}782\,661\,758(45) \times 10^{-36}\,\mathrm{kg}\)
Ve fyzice elementárních částic se klidová hmotnost udává běžně v jednotkách \(\mathrm{MeV}/c^2\), což odpovídá přibližně \(1{,}782\,662 \times 10^{-30}\,\mathrm{kg}\) (tj. zhruba dvojnásobek hmotnosti elektronu).
Hybnost
Hybnost fotonu je přímo úměrná jeho energii, přičemž konstantou úměrnosti je rychlost světla ve vakuu.
- \(p={E\over c}\)
Dle tohoto vztahu můžeme přirozeně měřit hybnost v jednotkách \(\mathrm{eV}/c\).
- \(1\,\mathrm{eV/c} = {1{,}602\,176\,487(40) \times 10^{-19}\,\mathrm{J} \over 299\,792\,458\,\mathrm{m/s} } = 5{,}344\,285\,50(13) \times 10^{-28}\,\mathrm{kg \cdot m \cdot s^{-1}}\)
Hybnost fotonu má v těchto jednotkách číselně stejnou hodnotu jako jeho energie. Výhodnost těchto jednotek lze demonstrovat na příkladu, kdy máme určit hybnost elektronu, který byl urychlen elektrickým napětím \(150\,\mathrm{kV}\). Podle definice elektronvoltu získal elektron kinetickou energii \(E_{\mathrm{k}}=150\,\mathrm{keV}\). Klidová hmotnost elektronu je \(m_{\mathrm{e}}=511\,\mathrm{keV}/c^2\), takže jeho energie v klidu je \(E_0=m_{\mathrm{e}} c^2 = 511\,\mathrm{keV}\). Celková energie urychlené částice je tedy jednoduše \(E = E_0 + E_{\mathrm{k}} = 661\,\mathrm{keV}\). K výpočtu hybnosti použijeme relativistický vztah známý jako Pythagorova věta o energii:
- \(E^2=E_0^2+\left(pc\right)^2 \,.\)
Odtud plyne
- \(pc = \sqrt{E^2-E_0^2} = \sqrt{661^2-511^2} \,\mathrm{keV} \;\dot=\; 419 \,\mathrm{keV}\).
Hybnost tedy můžeme zapsat jako \(p=419 \,\mathrm{keV}/c\). Je vidět, že konstanta \(c\) se ve vztazích chová tak, že ani není třeba znát její hodnotu a číselné operace jsou jednoduché.
Termodynamická teplota
Termodynamická teplota se místo kelvinů někdy udává v elektronvoltech. Převod je dán hodnotou Boltzmannovy konstanty \(k\).
- \(1\mathrm{eV}/k = {1\mathrm{eV} \over 8{,}617\,343(15) \times 10^{-5}\,\mathrm{eV/K}} = 11\,604{,}505(20)\,\mathrm{K}\)
Například teplotu v jádru Slunce 15,7 milionu kelvinů[10] lze zapsat jako \(1\,350\,\mathrm{eV}/k\). V tomto smyslu je povrchová teplota Slunce přibližně \(0{,}5\,\mathrm{eV}/k\). Po vynásobení faktorem \({3\over 2} k\) získáme střední kinetickou energii částic fotosféry \(0{,}75\,\mathrm{eV}\).[pozn 4]
Časy a vzdálenosti
U částic s velmi krátkou střední dobou života \(\tau\) se místo ní někdy udává tzv. rozpadová šířka, která má rozměr energie.
- \(\Gamma = {\hbar\over\tau}\)
Například mezon \(\mathrm{B^0}\) má dobu života asi 1,53 pikosekund,[11] čemuž odpovídá rozpadová šířka \(4{,}30 \times 10^{-4}\,\mathrm{eV}\). Je vidět, že časové údaje lze udávat v jednotkách \(\mathrm{eV^{-1}}\), či přesněji řečeno \(\mathrm{eV^{-1}}\hbar\).
- \(1\,\mathrm{eV^{-1}} \hbar = 6{,}582\,118\,99(16) \times 10^{-16} \,\mathrm{s}\)
A protože rychlost světla ve vakuu dává přímý přepočet mezi jednotkami času a vzdálenosti, je možné měřit i vzdálenost v jednotkách \(\mathrm{eV^{-1}}\), či přesněji zapsáno \(\mathrm{eV^{-1}} \hbar c\).
- \(1\,\mathrm{eV^{-1}} \hbar c = 1{,}973\,269\,631(49) \times 10^{-7} \,\mathrm{m}\)[2]
Vzhledem k typickým malým vzdálenostem ve světě částic, používá se tento vztah často ve tvarech[12]:
- \(1\,\mathrm{eV^{-1}} \hbar c = 197{,}326\,9631(49) \,\mathrm{nm} \,,\)
- \(1\,\mathrm{MeV^{-1}} \hbar c = 197{,}326\,9631(49) \,\mathrm{fm} \,.\)
Historie
Poprvé byla jednotka elektronvolt, tehdy ještě pod názvem „ekvivalent voltu“, použita roku 1912 v časopisu Philosophical Magazine v článku Karla Taylora Comptona a Owena Willanse Richardsona „The Photoelectric Effect“ o fotoelektrickém jevu.[13][14] V USA se s rozvojem částicové fyziky začala používat jednotka BeV (případně bev či Bev), kde B představovalo miliardu (z anglického „billion“). V roce 1948 však IUPAP její používání zamítl a naopak pro miliardu elektronvoltů upřednostnil použití předpony giga, takže jednotka je označována zkratkou GeV.[13] V některých starších publikacích se jako zkratka pro elektronvolt uvádí „ev“.[15] Od jednotky BeV byl odvozen název částicového urychlovače Bevatron (v provozu 1954–1993, Berkeley, USA). Podle stejného klíče byl pojmenován urychlovač Tevatron (od 1983, Illinois), který urychluje protony a antiprotony na energie až 1 TeV. Název Zevatron se někdy s nadsázkou užívá pro přírodní astrofyzikální zdroje částic s energiemi až 1021 eV (předpona zetta).[16] Vyšší energie jediné částice nebyla dosud nikdy zaznamenána.[17]
Poznámky
- ↑ Na obrázku je urychlující elektrické pole mezi elektrodami homogenní. Uvedené hodnoty energií ukazují, že kinetická energie částic přibývá přímo úměrně vzdálenosti od počáteční elektrody. Rychlost částic roste ve slabém poli kvadraticky, přičemž elektron na stejné vzdálenosti získá zhruba 43× vyšší rychlost. Proton získá 43× větší hybnost. Naznačené rychlosti částic nejsou v odpovídajícím poměru, ve skutečnosti by červená šipka měla být asi dvacetkrát menší, než je.
- ↑ 2,0 2,1 Tento článek používá vědecký zápis čísel. Závorkou je vyznačena směrodatná odchylka, která se týká vždy posledních dvou platných číslic. Všechny hodnoty uvedené včetně odchylek vychází z reference CODATA 2006.
- ↑ Uvedená hodnota \(hc\) vznikla vynásobením hodnoty \(\hbar c\) dle CODATA 2006 konstantou \(2\pi\) kvůli přepočtu \(\hbar\) na \(h\).
- ↑ Z historických a praktických důvodů není faktor ve vztahu mezi kinetickou energií a teplotou \(E_{\mathrm k} = 3/2\ kT\) roven jedné. Vymizí tak číselné konstanty v jiných vztazích, jako je např. stavová rovnice ideálního plynu, Boltzmannův faktor či Planckův vyzařovací zákon.
Reference
- ↑ Vyhláška Ministerstva průmyslu a obchodu o základních měřicích jednotkách a ostatních jednotkách a o jejich označování [online]. Ministerstvo průmyslu a obchodu, 14. července 2000, [cit. 2009-03-21]. Dostupné online.
- ↑ 2,0 2,1 2,2 2,3 MOHR, Peter J.; TAYLOR, Barry N.; NEWELL, David B.. CODATA recomended values of the fundamental physical constants: 2006. Review of Modern Physics, 2008-06-06, svazek 80, číslo 2, s. 709-714. Tabulka XLIX. Dostupné online [PDF, cit. 2009-03-21]. ISSN 1539-0756. DOI:10.1103/RevModPhys.80.633. (anglicky)
- ↑ TAYLOR, Barry N.; MOHR, Peter J.. Definitions of the SI units: Non-SI units [online]. NIST, 1998-02-17, rev. 2007-03-09, [cit. 2009-03-21]. (The NIST Reference on Constants, Units, and Uncertainty.) Sekce International System of Units from NIST. Dostupné online. (anglicky)
- ↑ CIPM, CCU, BIPM. SI brochure, Section 4.1, Non-SI units accepted for use with the SI, and units based on fundamental constants [online]. Sèvres Cedex, Francie : The International Bureau of Weights and Measures (Mezinárodní úřad pro míry a váhy), 2006-03, [cit. 2009-04-14]. Tabulka je taktéž dostupná online. Dostupné online. (anglicky)
- ↑ LHC Glossary, heslo TeV [online]. CERN, [cit. 2009-04-08]. Dostupné online. (anglicky)
- ↑ WAGNER, Vladimír. Jak se zkoumá narušení chirální symetrie aneb jak mi vládce podsvětí pomůže zjistit, proč má půvabná ženuška váží 64 kilo, místo méně než 1,4 kg, jak by se dalo očekávat [online]. 2001-10-25, [cit. 2009-04-14]. Příklad použití akronymu „mevů“. Psáno pro Neviditelného psa. Dostupné online. (česky)
- ↑ LHC Machine Outreach [online]. CERN, [cit. 2009-04-08]. Dostupné online. (anglicky)
- ↑ STAROBA, Pavel. Přirozená soustava jednotek [online]. Praha : České vysoké učení technické, 2008-09-29, [cit. 2009-04-08]. Dostupné online.
- ↑ NASA. Sun Fact Sheet [online]. 2004-09-01, rev. 2004-09-01, [cit. 2009-08-02]. Dostupné online. (anglicky)
- ↑ VANKOV, Peter Hristoforov. Study of the B-Meson Lifetime and the Performance of the Outer Tracker at LHCb [online]. CERN, 2008-11-05, [cit. 2009-04-08]. Dostupné online. (anglicky)
- ↑ AMSLER, Claude et al.. Review of Particle Physics. Physics Letters B, 2008-08-04, svazek 667, číslo 1. Particle Data Group, Physical constants, tabulka 1.1.. Dostupné online [PDF, cit. 2009-03-21]. ISSN 0370-2693. DOI:10.1016/j.physletb.2008.07.018. (anglicky)
- ↑ 13,0 13,1 MADORE, Barry F.. The Lexicon and Glossary of Terms in LEVEL 5, heslo Electron volt [online]. Pasadena, Kalifornie, USA : Caltech and Carnegie, 2002-08-14, rev. 2006-01-10, [cit. 2009-04-13]. Dostupné online. (anglicky)
- ↑ Editor. Electron volt [online]. Sizes, Inc, 2000, rev. 2004-11-26, [cit. 2009-04-14]. Dostupné online. (anglicky)
- ↑ National Research Council (U.S.). Conference on Glossary of Terms in Nuclear Science and Technology, National Research Council (U.S.). A glossary of terms in nuclear science and technology. New York : American Society of Mechanical Engineers, 1957. (anglicky)
- ↑ HONDA, Mitsuru; HONDA, Yasuko S.. Filamentary Jets as a Cosmic-Ray "Zevatron". The Astrophysical Journal, 2004-09-07, svazek 1, číslo 617, s. L37-L40. Dostupné online [PDF/HTML, cit. 2009-04-14]. ISSN 1538-4365. DOI:10.1086/427067. (anglicky)
- ↑ KULHÁNEK, Petr. Mohou Alfvénovy vlny i za vysoké energie v kosmickém záření?. Aldebaran Bulletin, 2009-04-17, ročník 2009, číslo 16. Dostupné online [cit. 2009-05-06]. ISSN 1214-1674.
Externí odkazy
- Český metrologický institut: Povolené jednotky mimo SI
- Jiří Bureš, converter.cz: Práce a energie - převodní tabulky veličin
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |