Multimediaexpo.cz je již 18 let na českém internetu !!
Sférická soustava souřadnic
Z Multimediaexpo.cz
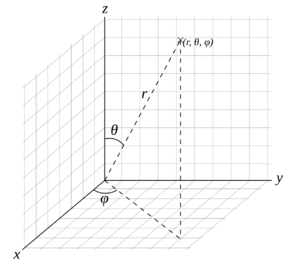
Sférická soustava souřadnic (kulová soustava souřadnic) je soustava souřadnic v prostoru, u které jedna souřadnice (označovaná \(r\)) udává vzdálenost bodu od počátku souřadnic, druhá souřadnice (označovaná \(\varphi\)) udává úhel odklonu průvodiče bodu od osy \(x\) a třetí souřadnice (označovaná \(\theta\)) úhel mezi průvodičem a osou \(z\).
Sférická soustava souřadnic je vhodná v případech takových problémů, které mají sférickou symetrii. Tyto mají zpravidla ve sférických souřadnicích podstatně jednodušší tvar.
Transformace sférických souřadnic na kartézské:
- \(x = r \sin{\theta} \cos{\varphi}\)
- \(y = r \sin{\theta} \sin{\varphi}\)
- \(z = r \cos{\theta}\,\)
Převod kartézských souřadnic na sférické:
- \(r = \sqrt{x^2 + y^2 + z^2},\)
- \(\varphi = \operatorname{arctg2}(y,x),\)
- \(\theta = \arccos\left(\frac{z}{r}\right),\)
kde arctg2(x,y) je zobecnění funkce arkus tangens. Úhly volíme v rozsahu \(0\leq\theta\leq\pi\) a \(0\leq\varphi<2\pi\).
Jakobián transformace z kartézské do sférické soustavy souřadnic :
\(J= r^2 \sin \theta \)
Délka infinitesimální úsečky se spočte jako
- \(\mathrm{d}s^2=\mathrm{d}r^2+r^2\mathrm{d}\theta^2 + r^2 \sin^2 \theta\ \mathrm{d}\varphi^2.\)
Objem infinitesimálního elementu prostoru spočteme jako
- \(\mathrm{d}V=r^2 \left|\sin\theta\right|\mathrm{d}r\,\mathrm{d}\varphi\,\mathrm{d}\theta,\)
takže celkový objem spočteme integrací tohoto výrazu přes danou oblast vyjádřenou ve sférických souřadnicích.
Externí odkazy
|
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |