Šestiúhelníkové číslo
Z Multimediaexpo.cz
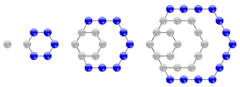
Šestiúhelníková čísla jsou figurální čísla odpovídající šestiúhelníku. Konkrétně je šestiúhelníkové číslo rovno počtu bodů, ze kterých lze sestavit pravidelný šestiúhelník dle obrázku.
Vzorec pro \(n\)-té šestiúhelníkové číslo \(h_n\) je
\(h_n= 2n^2-n = n(2n-1) = {{2n}\times{(2n-1)}\over 2}.\,\!\)
Několik prvních šestiúhelníkových čísel je 1, 6, 15, 28, 45, 66, 91, 120, 153, 190, 231, 276, 325, 378, 435, 496, 561, 630, 703, 780, 861, 946, atd.
Každé šestiúhelníkové číslo je zároveň trojúhelníkové číslo, ale jenom každé druhé trojúhelníkové číslo je šestiúhelníkové.
Stejně jako u trojúhelníkových čísel, může být ciferace šestiúhelníkového čísla (v desítkové soustavě) pouze 1, 3, 6 nebo 9, a to v pořadí 1, 6, 6, 1, 9, 3, 1, 3, 9, atd.
Všechna sudá dokonalá čísla jsou šestiúhelníková. Jsou dána vzorcem
\(M_p 2^{p-1} = M_p (M_p + 1)/2 = h_{(M_p+1)/2}=h_{2^{p-1}},\)
kde \(M_p\) je Mersennovo prvočíslo. Např. druhé šestiúhelníkové číslo je \(2\cdot 3 = 6\), čtvrté je \(4\cdot 7 = 28\), šestnácté je \(16\cdot 31 = 496\) a šedesátéčtvrté je \(64\cdot 127 = 8\,128\).
Protože nejsou známa žádná lichá dokonalá čísla, tak jsou všechna známá dokonalá čísla šestiúhelníková.
Největší přirozené číslo, které nelze zapsat jako součet nejvýše čtyř šestiúhelníkových čísel, je 130.
Adrien-Marie Legendre v roce 1830 dokázal, že se takto dají vyjádřit všechna přirozená čísla větší než 1 791.
Test šestiúhelníkovosti čísel
Zda je přirozené číslo \(x\) šestiúhelníkové, lze snadno zjistit vypočítáním hodnoty následujícího výrazu
\(n = \frac{\sqrt{8x+1}+1}{4}.\)
Pokud je \(n\) celé číslo, \(x\) je šestiúhelníkové číslo, jinak \(x\) šestiúhelníkovým číslem není.
Ostatní vlastnosti
Alternativně lze \(n\)-té šestiúhelníkové číslo vyjádřit jako součet
\( h_n = \sum_{i=0}^{n-1}{(4i+1)}. \)
Externí odkazy
|
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |