Intenzita magnetického pole

Z Multimediaexpo.cz

Intenzita magnetického pole je vektorová veličina popisující míru silových účinků magnetického pole. Na rozdíl od magnetické indukce nezahrnuje vliv vázaných magnetizačních proudů prostředí, ale pouze "vnějších" zdrojů pole, tedy volných elektrických proudů.

Značení a jednotky

• Doporučené značení:^[1] H
• Jednotka SI^[1]: ampér na metr, značka A/m.

Důležité vztahy

Základním obecným vztahem pro intenzitu stacionárního magnetického pole buzeného (ustáleným) volným elektrickým proudem I_vol je Ampérův zákon:

\(\oint_c \mathbf{H} \cdot \mathrm{d}\mathbf{l} = I_{\mathrm{vol}} \), kde integrace probíhá podle délky l libovolně zvolené uzavřené křivky c obemykající volný elektrický proud.

V oblastech prostoru, kde lze považovat prostorové rozložení elektrického proudu za spojité (v makroskopickém smyslu), popsatelné hustotou elektrického proudu, lze Ampérův zákon přepsat do diferenciálního tvaru:

\(\operatorname{rot}\,\mathbf{H} = \mathbf{j}_{\mathrm{vol}}\).

V nestacionárním poli pak platí první Maxwellova rovnice, která je definičním vztahem pro intenzitu magnetického pole v soustavě SI^[1] (S je obsah plochy ohraničené křivkou c, D je elektrická indukce):

\(\oint_c \mathbf{H} \cdot \mathrm{d}\mathbf{l} = \int_S (\mathbf{j}_{\mathrm{vol}}+ \frac{\partial}{\partial t}\mathbf{D}) \cdot \mathrm{d} \mathbf{S}\)

resp. v diferenciálním tvaru:

\( \operatorname{rot}\,\mathbf{H} = \mathbf{j}_{\mathrm{vol}} + \frac{\partial \mathbf{D}} {\partial t} \).

Vztah k magnetické indukci B:

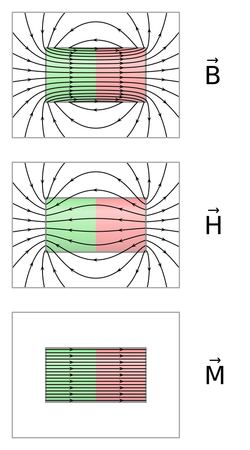
\(\mathbf{H} = \frac{\mathbf{B}}{\mu_0} - \mathbf{M}\), kde M je magnetizace, charakterizující účinky vázaných magnetizačních proudů.

Intenzitu stacionárního magnetického pole vytvořeného lineárním vodičem protékaným proudem udává Biotův–Savartův zákon:

\(\mathbf{H}(\mathbf{r}) = \frac{I}{4\pi}\int \mathrm{d}{\mathbf{r}'}\times\frac{(\mathbf{r}-\mathbf{r}')}{\vert \mathbf{r}-\mathbf{r}'\vert ^3}\;\), kde integrace probíhá přes všechny body \(\mathbf{r}' \,\) křivky proudovodiče,

resp. pro spojitě rozložený proud s hustotou \(\mathbf{j} \,\):

\(\mathbf{H}(\mathbf{r}) = \frac{1}{4\pi}\iiint\mathbf{j}(\mathbf{r}')\times\frac{(\mathbf{r}-\mathbf{r}')}{\vert \mathbf{r}-\mathbf{r}'\vert ^3}\;\mathrm{d}^3{\mathbf{r}'}\), kde integrace probíhá přes všechny body \(\mathbf{r}' \,\) oblasti protékané proudem.

Analogie s elektrostatickým polem

Z historických důvodů, od doby, kdy magnetismus byl vysvětlován fluidovou teorií, odpovídají pojmy a vztahy mezi intenzitou magnetického pole a magnetickou indukcí stacionárního magnetického pole obdobným vztahům z elektrostatiky mezi intenzitou elektrického pole a elektrickou indukcí. Tato analogie je pouze formální, nikoli fyzikální. Ve skutečnosti jsou základními vektory polí intenzita elektrického pole a magnetická indukce, popisující skutečné silové účinky celkového pole v prostředí. Intenzita magnetického pole je pak obdobná elektrické indukci, neboť obě odhlížejí od účinků dodatečných polí vzniklých v prostředí a popisují pole jako účinky pouze volných proudů resp. volných nábojů. Obě tyto veličiny tak doplňují popis polí v látkovém prostředí a jsou výhodné pro praktické výpočty vzhledem ke svému bezprostřednějšímu vztahu k makroskopickým zdrojům polí.^[2][3] Dokládá to např. výše uvedený Biotův–Savartův zákon, který umožňuje výpočet magnetického pole elektrického proudu, aniž by byla nutná znalost magnetických vlastností prostředí.

Hranice použitelnosti

Vzhledem k tomu, že intenzita magnetického pole je definována pomocí první Maxwellovy rovnice, vyplývají pro ni podobná omezení jako pro tuto rovnici. Polarizační proudy jsou započteny na pravé straně rovnice, naopak magnetizační na levé straně ("skryté" v intenzitě magnetického pole). Ve velmi rychle proměnném elektromagnetickém poli však nelze vázané proudy rozdělit na "posuvné" polarizační a uzavřené magnetizační proudy, neboť podstatné změny pole proběhnou za kratší čas, než je charakteristický čas pro uzavření magnetizačního proudu. V takovém případě se všechny vázané proudy jeví jako polarizační a magnetizaci a tedy ani intenzitu magnetického pole nelze rozumně definovat. I polarizace a elektrická indukce tím získávají odlišný charakter. Elektromagnetické pole se pak zpravidla popisuje pomocí 3 vektorových veličin: intenzity elektrického pole, magnetické indukce a oné pozměněné elektrické indukce, pro které se formulují pozměněné Maxwellovy rovnice.^[4]

Související články

• Magnetické pole
• Magnetická indukce
• Magnetizace (veličina)

Reference

1. ↑ ^{1,0 1,1 1,2} ČSN ISO 31-5 Veličiny a jednotky: Elektřina a magnetismus, Český normalizační institut, Praha 1994
2. ↑ SEDLÁK, Bedřich; ŠTOLL, Ivan. Elektřina a magnetismus. 1. vyd. Praha : Academia a Karolinum, 1993. 600 s. ISBN 80-200-0172-7. Kapitola 3.5.6, s. 236.  
3. ↑ HORÁK, Zdeněk; KRUPKA, František. Fyzika. Příručka pro vysoké školy technického směru. 3. vyd. Praha : SNTL/ALFA, 1981. 04-017-81. Kapitola 6.10.3, 6.11.7, s. 635, 657–9. (česky) 
4. ↑ BREDOV, M. M.; RUMJANCEV, V. V.; TOPTYGIN, I. N.. Klassičeskaja elektrodinamika. 1. vyd. Moskva : Nauka, 1985. 400 s. Část II, hlava I., § 2.2, s. 200–201. (rusky) 

Flickr.com nabízí fotografie, obrázky a videa k tématu Intenzita magnetického pole

Commons nabízí fotografie, obrázky a videa k tématu Intenzita magnetického pole

Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010
Informace o článku. Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. Tento text je dostupný za podmínek Creative Commons 3.0 Unported – creativecommons.org. Originální článek na české Wikipedii