Multimediaexpo.cz je již 18 let na českém internetu !!
V tiskové zprávě k 18. narozeninám brzy najdete nové a zásadní informace.
Exponenciální rozdělení
Z Multimediaexpo.cz
(+ Masivní vylepšení) |
m (Nahrazení textu „<math>“ textem „<big>\(“) |
||
| Řádka 3: | Řádka 3: | ||
==Definice== | ==Definice== | ||
| - | Spojitá náhodná proměnná < | + | Spojitá náhodná proměnná <big>\(X</math> má exponenciálně rozdělení s parametrem <big>\(\lambda > 0</math> právě tehdy, jestliže její hustota pravděpodobnosti má následující tvar: |
| - | :< | + | :<big>\(f_{X}(x) = \begin{cases}\lambda e^{-\lambda x} &; x \ge 0, \\0 &; x < 0.\end{cases}</math> |
Označujeme: | Označujeme: | ||
| - | * < | + | * <big>\(\operatorname X \sim Exp(\lambda)</math> |
== Základní charakteristiky rozdělení == | == Základní charakteristiky rozdělení == | ||
[[Střední hodnota]]: | [[Střední hodnota]]: | ||
| - | :< | + | :<big>\(E[X] = \frac{1}{\lambda}</math> |
[[Rozptyl]]: | [[Rozptyl]]: | ||
| - | :< | + | :<big>\(D[X] = \frac{1}{\lambda^2}</math> |
[[Koeficient šikmosti]]: | [[Koeficient šikmosti]]: | ||
| - | :< | + | :<big>\(\operatorname\gamma_{1} = 2</math> |
[[Momentová vytvořující funkce]]: | [[Momentová vytvořující funkce]]: | ||
| - | :< | + | :<big>\(m(t) = \frac{\lambda}{\lambda - t}</math> |
[[Distribuční funkce]]: | [[Distribuční funkce]]: | ||
| - | : < | + | : <big>\(F(x) = \begin{cases} 1-e^{-\lambda x} &; x \ge 0, \\ 0 &; x < 0.\end{cases}</math> |
==Zdroje== | ==Zdroje== | ||
Verze z 14. 8. 2022, 14:48
Exponenciální rozdělení či exponenciální pravděpodobnostní rozdělení je v teorii pravděpodobnosti a matematické statistice spojité rozdělení pravděpodobnosti. Exponenciální rozdělení vyjadřuje čas mezi náhodně se vyskytujícími událostmi. Využívá se například v pojistné matematice při určování (pravděpodobnostního) rozdělení výše pojistného plnění nebo času mezi nastalé pojistných událostí, dále například ve fyzice při modelování času radioaktivního rozpadu a v systémech hromadné obsluhy.
Obsah |
Definice
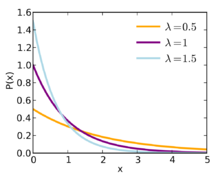
Spojitá náhodná proměnná \(X</math> má exponenciálně rozdělení s parametrem \(\lambda > 0</math> právě tehdy, jestliže její hustota pravděpodobnosti má následující tvar:
- \(f_{X}(x) = \begin{cases}\lambda e^{-\lambda x} &; x \ge 0, \\0 &; x < 0.\end{cases}</math>
Označujeme:
- \(\operatorname X \sim Exp(\lambda)</math>
Základní charakteristiky rozdělení
- \(E[X] = \frac{1}{\lambda}</math>
- \(D[X] = \frac{1}{\lambda^2}</math>
- \(\operatorname\gamma_{1} = 2</math>
- \(m(t) = \frac{\lambda}{\lambda - t}</math>
- \(F(x) = \begin{cases} 1-e^{-\lambda x} &; x \ge 0, \\ 0 &; x < 0.\end{cases}</math>
Zdroje
- http://iastat.vse.cz/Exponenc.htm
- http://home.zcu.cz/~friesl/hpsb/exp.html
- http://homel.vsb.cz/~dor028/Vybrana_rozdeleni_prsti.doc
Externí odkazy
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |