Gravitační čočka
Z Multimediaexpo.cz
m (Nahrazení textu „<math>“ textem „<big>\(“) |
m (Nahrazení textu „</math>“ textem „\)</big>“) |
||
| Řádka 21: | Řádka 21: | ||
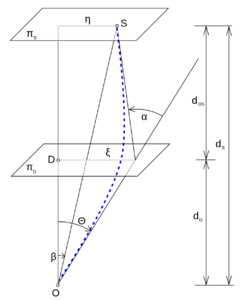
[[Soubor:gravitacni_cocka.png|thumb|240px|Princip gravitačního čočkování:<br />''S'' – zdroj světla<br />''D'' – gravitační čočka<br />''O'' – pozorovatel<br />π<sub>S</sub> – rovina zdroje<br /> | [[Soubor:gravitacni_cocka.png|thumb|240px|Princip gravitačního čočkování:<br />''S'' – zdroj světla<br />''D'' – gravitační čočka<br />''O'' – pozorovatel<br />π<sub>S</sub> – rovina zdroje<br /> | ||
π<sub>D</sub> – rovina čočky]] | π<sub>D</sub> – rovina čočky]] | ||
| - | Při vhodné [[poloha|poloze]] [[zdroj světla|zdroje světla]] <big>\(S</ | + | Při vhodné [[poloha|poloze]] [[zdroj světla|zdroje světla]] <big>\(S\)</big>, zdroje ohýbajícího [[gravitační pole|gravitačního pole]] <big>\(D\)</big> a [[pozorovatel]]e <big>\(O\)</big> dochází ke gravitačnímu čočkování. |
| - | Uvažujme uspořádání uvedené na [[:Soubor:gravitacni_cocka.png|obrázku]]. [[Světelný paprsek]] pocházející ze zdroje <big>\(S</ | + | Uvažujme uspořádání uvedené na [[:Soubor:gravitacni_cocka.png|obrázku]]. [[Světelný paprsek]] pocházející ze zdroje <big>\(S\)</big> je gravitační čočkou <big>\(D\)</big> ohnut o [[úhel]] <big>\(\alpha\)</big>. |
| - | [[Úhel]] <big>\(\beta</ | + | [[Úhel]] <big>\(\beta\)</big> je úhlem mezi spojnicí pozorovatele a čočky a spojnicí pozorovatele a zdroje. Pokud by se neprojevoval efekt gravitační čočky, byl by zdroj pozorován právě pod tímto úhlem. Přítomnost gravitační čočky však způsobí, že pro pozorovatele se obraz zdroje nachází pod úhlem <big>\(\Theta\)</big>. |
| - | Pro malé úhly lze položit <big>\(\Theta = \beta d_S+\alpha d_{DS}</ | + | Pro malé úhly lze položit <big>\(\Theta = \beta d_S+\alpha d_{DS}\)</big>. Poloha obrazu a zdroje jsou tedy vázány tzv. ''(gravitační) čočkovou rovnicí'' |
| - | :<big>\(\beta = \Theta - \alpha(\Theta)\frac{d_{DS}}{d_S}</ | + | :<big>\(\beta = \Theta - \alpha(\Theta)\frac{d_{DS}}{d_S}\)</big> |
| - | Tato rovnice je [[nelineární rovnice|nelineární]], takže určité pozici <big>\(\beta</ | + | Tato rovnice je [[nelineární rovnice|nelineární]], takže určité pozici <big>\(\beta\)</big> zdroje může odpovídat několik [[optický obraz|obrazů]] <big>\(\Theta\)</big>. V případě výskytu více obrazů lze pomocí [[Fermatův princip|Fermatova principu]] (za předpokladu, že [[index lomu]] nahradíme [[gravitační potenciál|newtonovským gravitačním potenciálem]] <big>\(\varphi\)</big> podle <big>\(n=1+\frac{2\varphi}{c^2}\)</big>) získat výrazy pro [[čas]]ové rozdíly v příchodech obou signálů, což lze vyjádřit jako |
| - | :<big>\(c\Delta t = \frac{d_D d_S}{2d_{DS}}{(\Theta-\beta)}^2 - \psi(\xi) + \mbox{konst}</ | + | :<big>\(c\Delta t = \frac{d_D d_S}{2d_{DS}}{(\Theta-\beta)}^2 - \psi(\xi) + \mbox{konst}\)</big>, |
| - | kde <big>\(\psi(\xi)</ | + | kde <big>\(\psi(\xi)\)</big> je tzv. ''ohybový (deflekční) potenciál''. Deflekční potenciál nezávisí na <big>\(\eta\)</big>. |
| - | V případě speciální polohy zdroje, čočky a pozorovatele, kdy <big>\(\beta=0</ | + | V případě speciální polohy zdroje, čočky a pozorovatele, kdy <big>\(\beta=0\)</big>, bude mít obraz tvar [[kruh|kruhového]] proužku (tzv. [[Einsteinův prstýnek]]) s [[poloměr]]em |
| - | :<big>\(\Theta_E = \sqrt{\frac{4\varkappa M}{c^2}\frac{d_{DS}}{d_D d_S}}</ | + | :<big>\(\Theta_E = \sqrt{\frac{4\varkappa M}{c^2}\frac{d_{DS}}{d_D d_S}}\)</big>, |
| - | kde <big>\(M</ | + | kde <big>\(M\)</big> je [[hmotnost]] čočky. |
| - | Není-li přesně <big>\(\beta=0</ | + | Není-li přesně <big>\(\beta=0\)</big>, rozpadá se prstýnek na dva kruhové [[oblouk]]y. Při ještě větší nepřesnosti seřazení objektů se objevují dva nebo více obrazů na různých stranách čočkujícího objektu. |
| - | Pokud jsou úhly ohybu <big>\(\alpha</ | + | Pokud jsou úhly ohybu <big>\(\alpha\)</big> velmi malé, způsobí gravitační čočka pouze určité zvětšení zdroje. Vzhledem ke vzájemnému pohybu čočky a zdroje může docházek k pozorování změn jasnosti zdroje. Průběh změn jasnosti v čase může poskytnout informace o hmotnosti čočkujícího objektu. Tento jev se označuje jako mikročočkování. |
==Historie== | ==Historie== | ||
Aktuální verze z 14. 8. 2022, 14:51
Gravitační čočka je astronomický pojem užívaný pro objekt s intenzivním gravitačním polem, který se nachází mezi pozorovatelem a zdrojem světla či jiného záření, přičemž tento objekt svým gravitačním polem zakřivuje paprsky vycházející ze zdroje podobně, jak tomu je u spojné čočky.
Proces ohybu světla v gravitačním poli (a jevy s ním související) se označují jako gravitační čočkování. Ohyb světla v gravitačním poli byl předpovězen na základě obecné teorie relativity.
Obsah |
Popis
Gravitační čočkou může být libovolný velmi hmotný objekt, např. černá díra, supermasivní černá díra, obří eliptická galaxie, hnízdo galaxií nebo kvasar.
Velikost ohybu světla závisí na vzdálenosti procházejícího paprsku od gravitační čočky - k největšímu ohybu dochází v těsné blízkosti objektu a se vzdáleností se vliv čočky změnšuje, takže v určité vzdálenosti jej lze již zanedbat (to je rozdíl oproti klasické optické čočce). Důsledkem této skutečnosti je to, že paprsky procházející v různých vzdálenostech mají různá ohniska.
Pokud se pozorovatel, zdroj a gravitační čočka nachází na společné ose, bude se pozorovateli zdroj světla jevit jako kroužek obepínající gravitační čočku. Tento jev je v gravitačním čočkování poměrně výjimečný a bývá označován jako Einsteinův prstýnek. Běžnější je případ, kdy gravitační čočka neleží přímo na ose spojující pozorovatele a zdroj. V tomto případě může vzniknou více obrazů zdroje v závislosti na poloze gravitační čočky.
Rozlišují se tři druhy gravitačního čočkování:
- silné čočkování - U silného čočkování jsou dobře rozlišitelné jednotlivé obrazy. V tomto případě bývá gravitační čočkou galaxie nebo kupa galaxií a zdrojem světla kvasar nebo galaxie.
- slabé čočkování - Při slabém čočkování dochází k pouze k malému narušení světelných zdrojů, které lze zjistit pouze analýzou velkého počtu objektů.
- mikročočkování - U mikročočkování splývají jednotlivé obrazy do jednoho světelného bodu. V tomto případě je obvykle čočkou hvězda.
Čočková rovnice
Při vhodné poloze zdroje světla \(S\), zdroje ohýbajícího gravitačního pole \(D\) a pozorovatele \(O\) dochází ke gravitačnímu čočkování.
Uvažujme uspořádání uvedené na obrázku. Světelný paprsek pocházející ze zdroje \(S\) je gravitační čočkou \(D\) ohnut o úhel \(\alpha\).
Úhel \(\beta\) je úhlem mezi spojnicí pozorovatele a čočky a spojnicí pozorovatele a zdroje. Pokud by se neprojevoval efekt gravitační čočky, byl by zdroj pozorován právě pod tímto úhlem. Přítomnost gravitační čočky však způsobí, že pro pozorovatele se obraz zdroje nachází pod úhlem \(\Theta\).
Pro malé úhly lze položit \(\Theta = \beta d_S+\alpha d_{DS}\). Poloha obrazu a zdroje jsou tedy vázány tzv. (gravitační) čočkovou rovnicí
- \(\beta = \Theta - \alpha(\Theta)\frac{d_{DS}}{d_S}\)
Tato rovnice je nelineární, takže určité pozici \(\beta\) zdroje může odpovídat několik obrazů \(\Theta\). V případě výskytu více obrazů lze pomocí Fermatova principu (za předpokladu, že index lomu nahradíme newtonovským gravitačním potenciálem \(\varphi\) podle \(n=1+\frac{2\varphi}{c^2}\)) získat výrazy pro časové rozdíly v příchodech obou signálů, což lze vyjádřit jako
- \(c\Delta t = \frac{d_D d_S}{2d_{DS}}{(\Theta-\beta)}^2 - \psi(\xi) + \mbox{konst}\),
kde \(\psi(\xi)\) je tzv. ohybový (deflekční) potenciál. Deflekční potenciál nezávisí na \(\eta\).
V případě speciální polohy zdroje, čočky a pozorovatele, kdy \(\beta=0\), bude mít obraz tvar kruhového proužku (tzv. Einsteinův prstýnek) s poloměrem
- \(\Theta_E = \sqrt{\frac{4\varkappa M}{c^2}\frac{d_{DS}}{d_D d_S}}\),
kde \(M\) je hmotnost čočky.
Není-li přesně \(\beta=0\), rozpadá se prstýnek na dva kruhové oblouky. Při ještě větší nepřesnosti seřazení objektů se objevují dva nebo více obrazů na různých stranách čočkujícího objektu.
Pokud jsou úhly ohybu \(\alpha\) velmi malé, způsobí gravitační čočka pouze určité zvětšení zdroje. Vzhledem ke vzájemnému pohybu čočky a zdroje může docházek k pozorování změn jasnosti zdroje. Průběh změn jasnosti v čase může poskytnout informace o hmotnosti čočkujícího objektu. Tento jev se označuje jako mikročočkování.
Historie
Obecná teorie relativity předpovídá ohyb světla v gravitačním poli hmotných zdrojů. Tato teoretická předpověď byla potvrzena v roce 1919 během pozorování zatmění Sluncem, kdy Arthur Eddington pozoroval, že paprsky hvězd nacházejících se blízko Slunci byly mírně vychýleny z předpokládané polohy (hvězdy, jejichž světlo procházelo v blízkosti Slunce se tedy zdály být na jiném místě, než by být měly).
Albert Einstein si uvědomil, že při vhodném uspořádání zdroje světla, pozorovatele a objektu, který je zdrojem gravitačního pole, může tento objekt ohýbat světlo podobným způsobem, jako by se mezi zdrojem světla a pozorovatelem nacházela čočka. Článek o tomtu jevu publikoval Einstein v roce 1937. Einstein předpokládal, že tento jev bude vzácný a je nepravděpodobné, že jej bude možné pozorovat.
Světlo v okolí velmi hmotného objektu může být ohnuto natolik, že se kolem něj několikrát obtočí než se vydá směrem k pozorovateli. Při gravitačním čočkování je tedy možné pozorovat nejen jeden obraz, ale více obrazů jednoho světelného zdroje.
V roce 1937 navrhl Fritz Zwicky jako možný zdroj gravitačního pole pro gravitační čočkování galaxie, což podle jeho výpočtů mělo umožnit zachycení tohoto jevu.
První pozorování tohoto jevu se však podařilo až v roce 1979 při pozorování kvasaru Q0957+561. Mikročočkování bylo poprvé pozorováno v roce 1989 na kvasaru QSO2237+0305.
Související články
Externí odkazy
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |