Návštěvnost naší encyklopedie dnes trhá všechny historické rekordy.
Návštěvnost dne 25. února 2026 byla — 484 927 unikátních návštěvníků !
Návštěvnost dne 26. února 2026 byla — 479 665 unikátních návštěvníků !
Návštěvnost dne 5. března 2026 byla — 475 445 unikátních návštěvníků !
Návštěvnost dne 25. února 2026 byla — 484 927 unikátních návštěvníků !
Návštěvnost dne 26. února 2026 byla — 479 665 unikátních návštěvníků !
Návštěvnost dne 5. března 2026 byla — 475 445 unikátních návštěvníků !
Kosmická rychlost
Z Multimediaexpo.cz
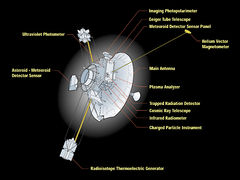
První umělá tělesa, která dosáhla 3. kosmické rychlosti a unikla tak z přitažlivostí Slunce, byly sondy Pioneer 10 a Pioneer 11.
Kosmická rychlost je rychlost, potřebná k překonání gravitačního působení kosmického tělesa.
Rozlišujeme několik kosmických rychlostí, běžně se setkáváme s prvními třemi:[1]
- 1. kosmická rychlost – rychlost, kterou potřebuje dosáhnout těleso zanedbatelné hmotnosti, aby obíhalo po kruhové dráze kolem planety; uvažujeme hodnotu na úrovni povrchu planety. Na Zemi tato rychlost činí 7,9 km/s.
- 2. kosmická rychlost – minimální úniková rychlost z povrchu planety. Pro Zemi je to přibližně 11,2 km/s, pro Měsíc 2,3 km/s, pro Jupiter 59,6, pro Slunce 617,3 km/s.
- 3. kosmická rychlost – rychlost potřebná k úniku z gravitačního působení Slunce. K odletu z míst oběžné dráhy Země je třeba rychlosti 42,1 km/s, lze však využít oběžné rychlosti planety Země, ta činí 29,8 km/s. Potřebná dodatečná rychlost tak klesne na 12,4 km/s. Raketa však musí překonat gravitační pole Země. Třetí kosmická rychlost proto je 16,7 km/s při startu ze zemského povrchu (tak se udává nejčastěji), případně 13,8 km/s pro odlet z vyčkávací dráhy kolem Země.
- 4. kosmická rychlost – rychlost potřebná k dosažení Slunce.[2] Pro start z povrchu Země je její hodnota 31,8 km/s.
- 5. kosmická rychlost – rychlost potřebná k úniku z gravitačního působení Slunce ve směru kolmém k rovině ekliptiky, pro start sondy z povrchu Země je její hodnota asi 52,8 km/s.
- 6. kosmická rychlost – rychlost potřebná k úniku z gravitačního působení Slunce ve směru proti oběhu Země okolo Slunce (rozdíl oproti 3. kosmické rychlosti). Na povrchu Země činí 72,8 km/s.
Reference
- ↑ MARTINEK, František, 1997: Z historie a současnosti kosmických raketoplánů (str. 7), Hvězdárna Valašské Meziříčí, ISBN 80-902445-2-1
- ↑ REICHL, Jaroslav; VŠETIČKA, Martin. Encyklopedie fyziky [online]. [cit. 2009-06-20]. Kapitola Třetí a čtvrtá komická rychlost. Dostupné online.
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |
