The final launch of the Allmultimedia.org will take place on February 27, 2026
(shortly after the 2026 Winter Olympics).
Eisensteinovo číslo
Z Multimediaexpo.cz
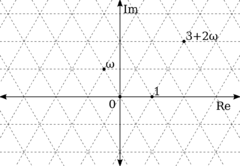
V matematice se jako Eisensteinova čísla, pojmenovaná po Ferdinandu Eisensteinovi (1823 – 1852), označují komplexní čísla tvaru
- \(z = a + b\omega \,\!\)
kde a a b jsou celá čísla a
- \(\omega = \frac{1}{2}(-1 + i\sqrt 3) = e^{2\pi i/3}\)
je (komplexní) třetí odmocnina z jedné. Podobně jako Gaussova čísla tvoří čtvercovou mříž, tvoří Eisensteinova čísla trojúhelníkovou mříž. Jedná se o okruh celistvých čísel číselného tělesa \(\mathbb{Q}\left(\mathrm i\sqrt{3}\right)\).
Dělitelnost
Na Eisensteinových číslech lze zavést dělitelnost stejně jako na celých číslech: \(x\) dělí \(y\) právě tehdy, existuje-li Eisensteinovo číslo \(z\) splňující \(y=zx\). To umožňuje převést z celých čísel i koncept prvočíselnosti, a mluvit o Eisensteinových prvočíslech.
Mezi Eisensteinovými čísly je celkem šest jednotek {±1, ±ω, ±ω2}, za Eisensteinova prvočíslo je tedy považováno každé takové Eisensteinovo číslo \(z\), které lze dělit pouze pouze jednotkami a prvky \(uz\), kde \(u\) je nějaká z jednotek.
Eisensteinova čísla tvoří komutativní okruh. Ten je dokonce eukleidovský, za eukleidovskou funkci je možno zvolit
- \(N(a + b\,\omega) = a^2 - a b + b^2. \,\!\)
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |
