The English encyclopedia Allmultimedia.org will be launched in two phases.
The final launch of the Allmultimedia.org will take place on February 24, 2026
(shortly after the 2026 Winter Olympics).

Eulerův vzorec

Z Multimediaexpo.cz

(Rozdíly mezi verzemi)
m (1 revizi)
(+ Masivní vylepšení)
Řádka 1: Řádka 1:
-
{{Wikipedia-cs|Eulerův vzorec|700}}
+
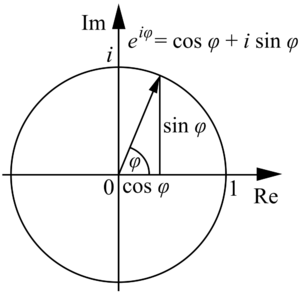
[[Soubor:Euler's formula.png|thumb|right|300px|Eulerův vzorec pro libovolný úhel.]]
 +
'''Eulerův vzorec''' určuje vztah mezi [[goniometrická funkce|goniometrickými funkcemi]] a [[exponenciální funkce|exponenciální funkcí]]:
 +
:<math>e^{i \phi} = \cos \phi + i \sin \phi \,\!</math>
 +
== Význam vzorce ==
 +
Je zvykem na Eulerův vzorec nahlížet jako na větu Komplexní analýzy. Pro jeho pochopení je potřeba vědět, co znamená mocnění komplexním číslem.
 +
 +
Uvažujme nejdříve exponenciální funkci reálné proměnné:
 +
 +
:<math>f(x) = e^{x}</math>
 +
 +
Ze znalosti [[Taylorova řada|Taylorovy řady]] víme, že:
 +
 +
:<math>e^{x} = \frac{x^0}{0!} +  \frac{x^1}{1!} + \frac{x^2}{2!} + ...</math>
 +
 +
Nyní si definujme exponenciální funkci komplexní proměnné tímto způsobem:
 +
 +
:<math>e^{a + bi} = \frac{{(a + bi)}^0}{0!} +  \frac{{(a + bi)}^1}{1!} + \frac{{(a + bi)}^2}{2!} + ...</math>
 +
 +
Dosaďme za exponent '''ix''':
 +
 +
:<math>e^{ix} = \frac{{(ix)}^0}{0!} +  \frac{{(ix)}^1}{1!} + \frac{{(ix)}^2}{2!} + \frac{{(ix)}^3}{3!} + ...</math>
 +
 +
Nyní mírně přerovnejme sčítance
 +
 +
:<math>e^{ix} = (\frac{{(ix)}^0}{0!} +  \frac{{(ix)}^2}{2!} + ...) + (\frac{{(ix)}^1}{1!} + \frac{{(ix)}^3}{3!} + ...)</math>
 +
 +
Ze druhé části vytkněme '''i''':
 +
 +
:<math>e^{ix} = (\frac{{(ix)}^0}{0!} +  \frac{{(ix)}^2}{2!} + ... ) + i(\frac{x^1}{1!} + \frac{i^2x^3}{3!} + ...)</math>
 +
 +
Teď se '''i''' vyskytuje pouze v sudých mocninách a můžeme ho umocnit:
 +
 +
:<math>e^{ix} = (\frac{x^0}{0!} -  \frac{x^2}{2!} + ... ) + i(\frac{x^1}{1!} - \frac{x^3}{3!} + ...)</math>
 +
 +
Ze znalosti [[Taylorova řada|Taylorovy řady]] víme, že první část je rozvoj funkce kosinus a druhá část je rozvoj funkce sinus:
 +
 +
:<math>e^{ix} = \cos(x) + i \sin(x)</math>
 +
 +
Ukázali jsme si, že při naší definici komplexního mocnění je Eulerův vzorec pravdivé tvrzení.
 +
 +
 +
{{Článek z Wikipedie}}
[[Kategorie:Rovnice]]
[[Kategorie:Rovnice]]

Verze z 30. 7. 2014, 19:58

Eulerův vzorec pro libovolný úhel.

Eulerův vzorec určuje vztah mezi goniometrickými funkcemi a exponenciální funkcí:

<math>e^{i \phi} = \cos \phi + i \sin \phi \,\!</math>

Význam vzorce

Je zvykem na Eulerův vzorec nahlížet jako na větu Komplexní analýzy. Pro jeho pochopení je potřeba vědět, co znamená mocnění komplexním číslem.

Uvažujme nejdříve exponenciální funkci reálné proměnné:

<math>f(x) = e^{x}</math>

Ze znalosti Taylorovy řady víme, že:

<math>e^{x} = \frac{x^0}{0!} + \frac{x^1}{1!} + \frac{x^2}{2!} + ...</math>

Nyní si definujme exponenciální funkci komplexní proměnné tímto způsobem:

<math>e^{a + bi} = \frac{{(a + bi)}^0}{0!} + \frac{{(a + bi)}^1}{1!} + \frac{{(a + bi)}^2}{2!} + ...</math>

Dosaďme za exponent ix:

<math>e^{ix} = \frac{{(ix)}^0}{0!} + \frac{{(ix)}^1}{1!} + \frac{{(ix)}^2}{2!} + \frac{{(ix)}^3}{3!} + ...</math>

Nyní mírně přerovnejme sčítance

<math>e^{ix} = (\frac{{(ix)}^0}{0!} + \frac{{(ix)}^2}{2!} + ...) + (\frac{{(ix)}^1}{1!} + \frac{{(ix)}^3}{3!} + ...)</math>

Ze druhé části vytkněme i:

<math>e^{ix} = (\frac{{(ix)}^0}{0!} + \frac{{(ix)}^2}{2!} + ... ) + i(\frac{x^1}{1!} + \frac{i^2x^3}{3!} + ...)</math>

Teď se i vyskytuje pouze v sudých mocninách a můžeme ho umocnit:

<math>e^{ix} = (\frac{x^0}{0!} - \frac{x^2}{2!} + ... ) + i(\frac{x^1}{1!} - \frac{x^3}{3!} + ...)</math>

Ze znalosti Taylorovy řady víme, že první část je rozvoj funkce kosinus a druhá část je rozvoj funkce sinus:

<math>e^{ix} = \cos(x) + i \sin(x)</math>

Ukázali jsme si, že při naší definici komplexního mocnění je Eulerův vzorec pravdivé tvrzení.


Citováno z „http://ww2000w.multimediaexpo.cz/mmecz/index.php/Euler%C5%AFv_vzorec“