V sobotu 2. listopadu proběhla mohutná oslava naší plnoletosti !!
Multimediaexpo.cz je již 18 let na českém internetu !!
Multimediaexpo.cz je již 18 let na českém internetu !!
Kružnice (graf)
Z Multimediaexpo.cz
(Rozdíly mezi verzemi)
m (1 revizi) |
m (Nahrazení textu „</math>“ textem „\)</big>“) |
||
| (Nejsou zobrazeny 2 mezilehlé verze.) | |||
| Řádka 1: | Řádka 1: | ||
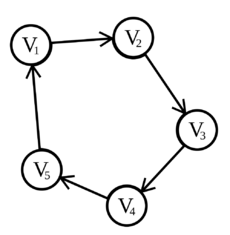
| - | + | [[Soubor:Orientovaná kružnice.png|thumb|230px|Orientovaná kružnice na pěti vrcholech.]] | |
| + | V [[teorie grafů|teorii grafů]] se termínem '''kružnice''' (též '''cyklus''') označuje takový [[Graf (teorie grafů)|graf]], který se skládá z jediného ''cyklu'' - tedy uzavřené [[posloupnost]]i propojených vrcholů. Kružnice může být [[orientovaný graf|orientovaná]] i neorientovaná. | ||
| + | Graf, který jako [[podgraf]] obsahuje kružnici, se nazývá '''cyklický'''. V opačném případě se nazývá '''acyklický''' (viz [[strom (graf)|strom]]). | ||
| + | |||
| + | == Definice == | ||
| + | Kružnice je graf <big>\(C_n = (V, E)\)</big>, kde <big>\(V = \left \{ v_1, \ldots, v_n \right \}\)</big> a <big>\(E = \left \{ e_1, \ldots, e_n \right \}\)</big> a platí: | ||
| + | ; orientovaný graf | ||
| + | : <big>\(e_i = \left( v_i, v_{i+1} \right), i = 1, \ldots, n - 1\)</big> a <big>\(e_n = \left( v_n, v_1 \right)\)</big> | ||
| + | : každý vrchol orientované kružice má vstupní i výstupní stupeň roven 1 | ||
| + | ; neorientovaný graf | ||
| + | : <big>\(e_i = \left \{ v_i, v_{i+1} \right \}, i = 1, \ldots, n - 1\)</big> a <big>\(e_n = \left \{ v_n, v_1 \right \}\)</big> | ||
| + | : každý vrchol neorientované kružnice má [[stupeň vrcholu|stupeň]] 2 | ||
| + | |||
| + | == Vlastnosti == | ||
| + | Kružnice je graf: | ||
| + | * [[souvislý graf|souvislý]] | ||
| + | * [[regulární graf|regulární]] | ||
| + | * [[eulerovský graf|eulerovský]] | ||
| + | * [[bipartitní graf|bipartitní]], obsahuje-li sudý počet vrcholů | ||
| + | |||
| + | |||
| + | {{Článek z Wikipedie}} | ||
| + | [[Kategorie:Typy grafů]] | ||
[[Kategorie:Grafové pojmy]] | [[Kategorie:Grafové pojmy]] | ||
Aktuální verze z 14. 8. 2022, 14:52
V teorii grafů se termínem kružnice (též cyklus) označuje takový graf, který se skládá z jediného cyklu - tedy uzavřené posloupnosti propojených vrcholů. Kružnice může být orientovaná i neorientovaná.
Graf, který jako podgraf obsahuje kružnici, se nazývá cyklický. V opačném případě se nazývá acyklický (viz strom).
Definice
Kružnice je graf \(C_n = (V, E)\), kde \(V = \left \{ v_1, \ldots, v_n \right \}\) a \(E = \left \{ e_1, \ldots, e_n \right \}\) a platí:
- orientovaný graf
- \(e_i = \left( v_i, v_{i+1} \right), i = 1, \ldots, n - 1\) a \(e_n = \left( v_n, v_1 \right)\)
- každý vrchol orientované kružice má vstupní i výstupní stupeň roven 1
- neorientovaný graf
- \(e_i = \left \{ v_i, v_{i+1} \right \}, i = 1, \ldots, n - 1\) a \(e_n = \left \{ v_n, v_1 \right \}\)
- každý vrchol neorientované kružnice má stupeň 2
Vlastnosti
Kružnice je graf:
- souvislý
- regulární
- eulerovský
- bipartitní, obsahuje-li sudý počet vrcholů
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |