V encyklopedii Allmultimedia.cz byl aktivován špičkový grafický skin Foreground.
Foreground plně podporuje – RWD, HTML 5.0, Super Galerii a YouTube 2.0 !

Kostra grafu

Z Multimediaexpo.cz

(Rozdíly mezi verzemi)
m (1 revizi)
(+ Aktualizace)
Řádka 1: Řádka 1:
-
{{Wikipedia-cs|Kostra grafu|700}}
+
[[Soubor:Spanning tree.png|thumb|240px|Kostra (červeně) grafu (černě)]]
 +
[[Soubor:Натурализация гамильтоновых циклов.jpg|thumb|240px|Tři příklady na mřížkovém grafu 8x8]]
 +
V [[teorie grafů|teorii grafů]] je '''kostra souvislého grafu ''G''''' takový [[podgraf]] [[Souvislý graf|souvislého grafu]] ''G'' na [[množina|množině]] všech jeho [[Graf (teorie grafů)#Základní pojmy|vrcholů]], který je [[strom (graf)|stromem]].
 +
== Příklady ==
 +
* [[Kružnice (graf)|Kružnice]] na ''n'' vrcholech (graf <big>\(C_n\)</big>) má právě ''n'' různých koster.
 +
* Libovolný [[strom (graf)|strom]] má jedinou kostru – sám sebe.
 +
* [[Úplný graf]] na ''n'' vrcholech má právě <big>\(n^{n-2}\)</big> různých koster (tzv. [[Cayleyho vzorec]]).
 +
 +
== Algoritmy pro hledání kostry ==
 +
=== Libovolná kostra ===
 +
Následující základní [[algoritmus]] je schopen nalézt nějakou (blíže neurčenou) kostru:
 +
# Nechť <big>\(G = (V, E)\)</big> je graf s ''n'' vrcholy a ''m'' [[Graf (teorie grafů)#Základní pojmy|hranami]]; seřaďme hrany G libovolně do [[posloupnost]]i <big>\((e_1, e_2, \ldots, e_m)\)</big>; položme <big>\(E_0 = \emptyset\)</big>.
 +
# Byla-li již nalezena [[množina]] <big>\(E_{i-1}\)</big>, spočítáme množinu <big>\(E_i\)</big> takto:
 +
#* <big>\(E_i = E_{i-1}\)</big> ∪ {<big>\(e_i\)</big>}, neobsahuje-li graf (V, <big>\(E_{i-1}\)</big> ∪ <big>\({e_i}\)</big>) kružnici,
 +
#* <big>\(E_i = E_{i-1}\)</big> jinak.
 +
# Algoritmus se zastaví, jestliže buď <big>\(E_i\)</big> již obsahuje ''n''&nbsp;−&nbsp;1 hran nebo ''i&nbsp;=&nbsp;m'', tedy se probraly všechny hrany z ''G''. Graf <big>\(T = (V, E_i)\)</big> pak představuje kostru grafu ''G''.
 +
 +
=== Minimální kostra ===
 +
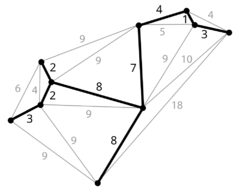
[[Soubor:Minimum spanning tree.png|thumb|240px|Minimální kostra grafu]]
 +
Je-li navíc definována funkce <big>\(w:\mathit{E}\rightarrow\mathbb{R}\)</big> (tzv. ''ohodnocení hran''), má smysl hledat '''minimální kostru''' – tedy takovou kostru <big>\((\mathit{V}, \mathit{E}')\)</big>, že výraz
 +
:<big>\(w(E') = \sum_{e \in \mathit{E}'} w(e)\)</big>
 +
nabývá ''minimální'' hodnoty.
 +
 +
Tuto úlohu řeší několik algoritmů, které jsou označovány jako [[hladový algoritmus|hladové]], neboť jednou provedená rozhodnutí už nikdy nemění, čili „hladově“ postupují přímo k řešení.
 +
 +
Předpokládejme, že je dán [[souvislý graf]] ''G = (V, E)'' s ohodnocením ''w'':
 +
 +
==== Kruskalův algoritmus ====
 +
{{Podrobně|Kruskalův algoritmus}}
 +
Předpokládejme navíc, že hrany jsou uspořádány tak, že platí <big>\(w(e_1) \le w(e_2) \le \ldots \le w(e_m)\)</big>.
 +
 +
Pro toto uspořádání provedeme algoritmus pro hledání libovolné kostry (viz výše).
 +
 +
==== Borůvkův algoritmus ====
 +
{{Podrobně|Borůvkův algoritmus}}
 +
 +
Předpokládejme, že ohodnocení hran v grafu je prosté. Algoritmus pracuje ve fázích tak, že postupně spojuje komponenty souvislosti (na počátku je každý vrchol komponentou souvislosti) do větších a větších celků, až zůstane jen jediný, a to je hledaná minimální kostra. V každé fázi vybere pro každou komponentu souvislosti hranu s co nejnižší cenou, která směřuje do jiné komponenty souvislosti a tu přidá do kostry.
 +
 +
==== Jarníkův algoritmus ====
 +
{{Podrobně|Jarníkův algoritmus}}
 +
# Nechť <big>\(|\mathit{V}| = n\)</big> a <big>\(|\mathit{E}| = m\)</big>. Položme <big>\(\mathit{E_0} = \empty\;, \mathit{V_0} = \{v\}\)</big>, kde ''v'' je libovolný vrchol ''G''.
 +
# Nalezneme hranu <big>\(e_i = \{x_i, y_i\} \in \mathit{E(G)}\)</big> nejmenší možné váhy z množiny hran takových, že <big>\(x_i \in \mathit{V}_{i-1}, y_i \in \mathit{V} \setminus \mathit{V}_{i-1}\)</big>.
 +
# Položíme <big>\(\mathit{V_i} = \mathit{V}_{i-1} \cup \{y_i\}\)</big> a <big>\(\mathit{E_i} = \mathit{E}_{i-1} \cup \{e_i\}\)</big>.
 +
# Pokud žádná taková hrana neexistuje, algoritmus končí a <big>\(T = (\mathit{V_i}, \mathit{E_i})\)</big>, jinak pokračuj krokem 2.
 +
 +
Nejrychlejší známý [[deterministický algoritmus]] pro hledání minimální kostry grafu vytvořil [[Bernard Chazelle]] modifikací Borůvkova algoritmu. [[Asymptotická složitost|Asymptotická časová složitost]] tohoto algoritmu je O(''E'' α(V)), kde α je inverzní [[Ackermannova funkce]].
 +
 +
== Literatura ==
 +
* Jiří Matoušek, Jaroslav Nešetřil: ''Kapitoly z diskrétní matematiky'', nakladatelství Karolinum, Praha 2002, ISBN: 80-246-0084-6
 +
* Jakub Černý: [https://web.archive.org/web/20071018060717/http://kam.mff.cuni.cz/~kuba/ka/ Základní grafové algoritmy] (PDF texty)
 +
 +
== Externí odkazy ==
 +
* [http://teorie-grafu.elfineer.cz/vybrane-problemy/minimalni-kostra.php Kruskalův algoritmus]- animace a příklady, bakalářská práce z MFF UK
 +
* [https://web.archive.org/web/20090120232242/http://www.zdenek-hejl.com/2009/01/link-building-maximalni-kostra-grafu.html Maximální kostra grafu] – využití algoritmu pro zjištění maximální kostry grafu pro link building
 +
 +
 +
{{Commonscat|Spanning trees}}{{Článek z Wikipedie}}
[[Kategorie:Grafové pojmy]]
[[Kategorie:Grafové pojmy]]

Verze z 30. 5. 2025, 10:53

Kostra (červeně) grafu (černě)
Tři příklady na mřížkovém grafu 8x8

V teorii grafů je kostra souvislého grafu G takový podgraf souvislého grafu G na množině všech jeho vrcholů, který je stromem.

Obsah

Příklady

  • Kružnice na n vrcholech (graf \(C_n\)) má právě n různých koster.
  • Libovolný strom má jedinou kostru – sám sebe.
  • Úplný graf na n vrcholech má právě \(n^{n-2}\) různých koster (tzv. Cayleyho vzorec).

Algoritmy pro hledání kostry

Libovolná kostra

Následující základní algoritmus je schopen nalézt nějakou (blíže neurčenou) kostru:

  1. Nechť \(G = (V, E)\) je graf s n vrcholy a m hranami; seřaďme hrany G libovolně do posloupnosti \((e_1, e_2, \ldots, e_m)\); položme \(E_0 = \emptyset\).
  2. Byla-li již nalezena množina \(E_{i-1}\), spočítáme množinu \(E_i\) takto:
    • \(E_i = E_{i-1}\) ∪ {\(e_i\)}, neobsahuje-li graf (V, \(E_{i-1}\) ∪ \({e_i}\)) kružnici,
    • \(E_i = E_{i-1}\) jinak.
  3. Algoritmus se zastaví, jestliže buď \(E_i\) již obsahuje n − 1 hran nebo i = m, tedy se probraly všechny hrany z G. Graf \(T = (V, E_i)\) pak představuje kostru grafu G.

Minimální kostra

Minimální kostra grafu

Je-li navíc definována funkce \(w:\mathit{E}\rightarrow\mathbb{R}\) (tzv. ohodnocení hran), má smysl hledat minimální kostru – tedy takovou kostru \((\mathit{V}, \mathit{E}')\), že výraz

\(w(E') = \sum_{e \in \mathit{E}'} w(e)\)

nabývá minimální hodnoty.

Tuto úlohu řeší několik algoritmů, které jsou označovány jako hladové, neboť jednou provedená rozhodnutí už nikdy nemění, čili „hladově“ postupují přímo k řešení.

Předpokládejme, že je dán souvislý graf G = (V, E) s ohodnocením w:

Kruskalův algoritmus

Podrobnější informace naleznete na stránce: Kruskalův algoritmus

Předpokládejme navíc, že hrany jsou uspořádány tak, že platí \(w(e_1) \le w(e_2) \le \ldots \le w(e_m)\).

Pro toto uspořádání provedeme algoritmus pro hledání libovolné kostry (viz výše).

Borůvkův algoritmus

Podrobnější informace naleznete na stránce: Borůvkův algoritmus


Předpokládejme, že ohodnocení hran v grafu je prosté. Algoritmus pracuje ve fázích tak, že postupně spojuje komponenty souvislosti (na počátku je každý vrchol komponentou souvislosti) do větších a větších celků, až zůstane jen jediný, a to je hledaná minimální kostra. V každé fázi vybere pro každou komponentu souvislosti hranu s co nejnižší cenou, která směřuje do jiné komponenty souvislosti a tu přidá do kostry.

Jarníkův algoritmus

Podrobnější informace naleznete na stránce: Jarníkův algoritmus
  1. Nechť \(|\mathit{V}| = n\) a \(|\mathit{E}| = m\). Položme \(\mathit{E_0} = \empty\;, \mathit{V_0} = \{v\}\), kde v je libovolný vrchol G.
  2. Nalezneme hranu \(e_i = \{x_i, y_i\} \in \mathit{E(G)}\) nejmenší možné váhy z množiny hran takových, že \(x_i \in \mathit{V}_{i-1}, y_i \in \mathit{V} \setminus \mathit{V}_{i-1}\).
  3. Položíme \(\mathit{V_i} = \mathit{V}_{i-1} \cup \{y_i\}\) a \(\mathit{E_i} = \mathit{E}_{i-1} \cup \{e_i\}\).
  4. Pokud žádná taková hrana neexistuje, algoritmus končí a \(T = (\mathit{V_i}, \mathit{E_i})\), jinak pokračuj krokem 2.

Nejrychlejší známý deterministický algoritmus pro hledání minimální kostry grafu vytvořil Bernard Chazelle modifikací Borůvkova algoritmu. Asymptotická časová složitost tohoto algoritmu je O(E α(V)), kde α je inverzní Ackermannova funkce.

Literatura

  • Jiří Matoušek, Jaroslav Nešetřil: Kapitoly z diskrétní matematiky, nakladatelství Karolinum, Praha 2002, ISBN: 80-246-0084-6
  • Jakub Černý: Základní grafové algoritmy (PDF texty)

Externí odkazy


Commons nabízí fotografie, obrázky a videa k tématu
Kostra grafu
Citováno z „http://ww2000w.multimediaexpo.cz/mmecz/index.php/Kostra_grafu“