Multimediaexpo.cz je již 18 let na českém internetu !!
Wheatstoneův můstek
Z Multimediaexpo.cz
m (1 revizi) |
m (Nahrazení textu „</math>“ textem „\)</big>“) |
||
| (Není zobrazena jedna mezilehlá verze.) | |||
| Řádka 4: | Řádka 4: | ||
== Zakreslení == | == Zakreslení == | ||
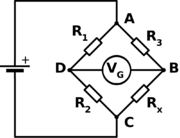
| - | Můstek se obvykle zakresluje způsobem zobrazeným v obrázku. Skládá se ze dvou větví (větev < | + | Můstek se obvykle zakresluje způsobem zobrazeným v obrázku. Skládá se ze dvou větví (větev <big>\(R_{1}\)</big>, <big>\(R_{2}\)</big> a větev <big>\(R_{3}\)</big>, <big>\(R_{x}\)</big>) připojených na stejnosměrný napájecí zdroj. Větve se chovají jako [[dělič napětí|děliče napětí]]. Zjednodušenou úvahou (pro případ odpojeného měřidla V<sub>G</sub>) snadno dojdeme k závěru, že pokud je [[Elektrické napětí|napětí]] mezi body D a B nulové (vyvážený můstek), musí platit: |
| - | < | + | <big>\(\frac{R_{1}}{R_{2}} = \frac{R_{3}}{R_{x}}\)</big>, z čehož pak pro neznámý odpor <big>\(R_{x} = \frac{R_{3} R_{2}}{R_{1}}\)</big> |
| - | Wheatstoneův můstek se používá i pro výchylková měření, kdy odpor < | + | Wheatstoneův můstek se používá i pro výchylková měření, kdy odpor <big>\(R_{x}\)</big> může být realizován například odporovým teploměrem, nebo odporovým [[tenzometr]]em. Výstupní napětí můstku (mezi body ''D'' a ''B'') je pak nelineární funkcí velikosti odporu <big>\(R_{x}\)</big>. |
== Reference == | == Reference == | ||
Aktuální verze z 14. 8. 2022, 14:54
Wheatstoneův můstek je obvod používaný pro měření odporu a malých změn odporu. Můstek vynalezl roku 1833 britský vědec a matematik Samuel Hunter Christie (1784-1865), ale zdokonalil jej a popularizoval až roku 1843 britský fyzik a vynálezce Sir Charles Wheatstone (1802–1875).
Zakreslení
Můstek se obvykle zakresluje způsobem zobrazeným v obrázku. Skládá se ze dvou větví (větev \(R_{1}\), \(R_{2}\) a větev \(R_{3}\), \(R_{x}\)) připojených na stejnosměrný napájecí zdroj. Větve se chovají jako děliče napětí. Zjednodušenou úvahou (pro případ odpojeného měřidla VG) snadno dojdeme k závěru, že pokud je napětí mezi body D a B nulové (vyvážený můstek), musí platit:
\(\frac{R_{1}}{R_{2}} = \frac{R_{3}}{R_{x}}\), z čehož pak pro neznámý odpor \(R_{x} = \frac{R_{3} R_{2}}{R_{1}}\)
Wheatstoneův můstek se používá i pro výchylková měření, kdy odpor \(R_{x}\) může být realizován například odporovým teploměrem, nebo odporovým tenzometrem. Výstupní napětí můstku (mezi body D a B) je pak nelineární funkcí velikosti odporu \(R_{x}\).
Reference
Související články
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |