Multimediaexpo.cz je již 18 let na českém internetu !!
Problém P versus NP
Z Multimediaexpo.cz
m (Nahrazení textu „<math>“ textem „<big>\(“) |
m (Nahrazení textu „</math>“ textem „\)</big>“) |
||
| Řádka 10: | Řádka 10: | ||
== Důsledky řešení == | == Důsledky řešení == | ||
| - | Platí-li '''P''' = '''NP''', má to dalekosáhlé důsledky. Mimo jiné by to znamenalo, že existují deterministické polynomiální (tedy „rychlé“) algoritmy na řešení všech [[NP-úplnost|NP-úplných]] problémů. To by mělo zásadní dopad nejen na teoretickou informatiku, logiku, ale také filosofii<ref>http://www.scottaaronson.com/papers/philos.pdf - Why Philosophers Should Care About Computational Complexity</ref> a zejména [[kryptografie|kryptografii]]. Obtížnost prolomení řady moderních šifer, které se dnes každodenně používají, totiž závisí na předpokladu, že platí nerovnost. NP-úplné problémy − mezi něž patří důležité praktické úlohy, jako např. [[problém obchodního cestujícího]] − jsou považovány za „těžké“ a předpokládá se, že žádný takový efektivní algoritmus pro ně neexistuje. To je také hlavní důvod, proč je dnes většina odborníků<ref>http://www.cs.umd.edu/~gasarch/papers/poll2012.pdf - SIGACT News Complexity Theory Column 74</ref> přesvědčena o tom, že rovnost neplatí, tedy že <big>\(P\neq NP</ | + | Platí-li '''P''' = '''NP''', má to dalekosáhlé důsledky. Mimo jiné by to znamenalo, že existují deterministické polynomiální (tedy „rychlé“) algoritmy na řešení všech [[NP-úplnost|NP-úplných]] problémů. To by mělo zásadní dopad nejen na teoretickou informatiku, logiku, ale také filosofii<ref>http://www.scottaaronson.com/papers/philos.pdf - Why Philosophers Should Care About Computational Complexity</ref> a zejména [[kryptografie|kryptografii]]. Obtížnost prolomení řady moderních šifer, které se dnes každodenně používají, totiž závisí na předpokladu, že platí nerovnost. NP-úplné problémy − mezi něž patří důležité praktické úlohy, jako např. [[problém obchodního cestujícího]] − jsou považovány za „těžké“ a předpokládá se, že žádný takový efektivní algoritmus pro ně neexistuje. To je také hlavní důvod, proč je dnes většina odborníků<ref>http://www.cs.umd.edu/~gasarch/papers/poll2012.pdf - SIGACT News Complexity Theory Column 74</ref> přesvědčena o tom, že rovnost neplatí, tedy že <big>\(P\neq NP\)</big>. |
== Související články == | == Související články == | ||
Aktuální verze z 14. 8. 2022, 14:53
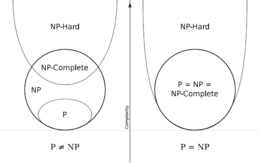
Problém P versus NP je důležitý otevřený problém v teoretické informatice; označuje se tak otázka, zda jsou třídy složitosti P a NP totožné. Zjednodušeně řečeno jde o otázku, zda každý problém, u kterého dokáže počítač rychle ověřit správnost nabídnutého řešení, dokáže počítač také sám rychle vyřešit. Všeobecně se předpokládá, že platí P ≠ NP, tedy že existují úlohy, které je složitější vyřešit než ověřit platnost řešení. Důkaz však stále nebyl nalezen a tento problém je zařazený mezi sedm tzv. problémů tisíciletí.
Obsah |
Popis tříd P a NP
Třída složitosti P obsahuje všechny úlohy, jejichž řešení lze nalézt deterministickým Turingovým strojem v polynomiálním čase.
Pro třídu NP platí totéž s tím rozdílem, že úlohy jsou v polynomiálním čase řešitelné hypotetickým nedeterministickým Turingovým strojem, který dokáže současně testovat mnoho možností řešení. Jsou to tedy ty problémy, jejichž řešení lze ověřit v polynomiálním čase, ovšem nevíme, zda je lze také v polynomiálním čase nalézt.
Třídy P a NP poprvé definoval americký informatik Stephen Cook.
Důsledky řešení
Platí-li P = NP, má to dalekosáhlé důsledky. Mimo jiné by to znamenalo, že existují deterministické polynomiální (tedy „rychlé“) algoritmy na řešení všech NP-úplných problémů. To by mělo zásadní dopad nejen na teoretickou informatiku, logiku, ale také filosofii[1] a zejména kryptografii. Obtížnost prolomení řady moderních šifer, které se dnes každodenně používají, totiž závisí na předpokladu, že platí nerovnost. NP-úplné problémy − mezi něž patří důležité praktické úlohy, jako např. problém obchodního cestujícího − jsou považovány za „těžké“ a předpokládá se, že žádný takový efektivní algoritmus pro ně neexistuje. To je také hlavní důvod, proč je dnes většina odborníků[2] přesvědčena o tom, že rovnost neplatí, tedy že \(P\neq NP\).
Související články
Reference
- ↑ http://www.scottaaronson.com/papers/philos.pdf - Why Philosophers Should Care About Computational Complexity
- ↑ http://www.cs.umd.edu/~gasarch/papers/poll2012.pdf - SIGACT News Complexity Theory Column 74
Externí odkazy
- R. Impagliazzo, A personal view of average-case complexity (PostScript)
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |