nová soutěž o nejlepší webovou stránku !!
Proto neváhejte a začněte rychle soutěžit o lákavé ceny !!
Integrálsinus
Z Multimediaexpo.cz
m (1 revizi) |
m (Nahrazení textu „</math>“ textem „\)</big>“) |
||
| (Nejsou zobrazeny 3 mezilehlé verze.) | |||
| Řádka 1: | Řádka 1: | ||
| - | {{ | + | {{Upravit}}[[Soubor:Sine integral.png|thumb|240px|Integrálsinus]] |
| + | '''Integrálsinus''' je definován jako [[integrál]] | ||
| + | <big>\(\operatorname{Si}\, x= \int_0^x \frac{\sin t}{t} dt = x - \frac{x^3}{3\cdot 3!}+\frac{x^5}{5\cdot 5!}-\frac{x^7}{7\cdot 7!}+\cdots\)</big>, | ||
| + | |||
| + | který není vyjádřitelný pomocí [[elementární funkce|elementárních funkcí]]. Řada byla získána prostým integrováním [[mocninná řada|mocninné řady]] pro <big>\(\frac{\sin x}{x}\)</big> člen po členu. | ||
| + | |||
| + | Z tvaru mocninné řady je zřejmé, že jde o funkci [[lichá funkce|lichou]]. Pro <big>\(x>0\)</big> má [[extrém funkce|extrémy]] v bodech <big>\(n\pi\)</big>, kde <big>\(n\)</big> je přirozené číslo. | ||
| + | |||
| + | Přičemž lichým <big>\(n\)</big> odpovídají maxima a sudým minima. | ||
| + | |||
| + | Například pomocí [[reziduová věta|reziduové věty]] lze vypočítat, že | ||
| + | |||
| + | <big>\(\lim_{x\to \infty} \operatorname{Si}\, x = \int_0^{\infty}\frac{\sin t}{t} dt = \frac{\pi}{2}\)</big> | ||
| + | |||
| + | |||
| + | {{Článek z Wikipedie}} | ||
[[Kategorie:Integrální počet]] | [[Kategorie:Integrální počet]] | ||
Aktuální verze z 14. 8. 2022, 14:52
| Tento článek potřebuje úpravy. Můžete Multimediaexpo.cz pomoci tím, že ho vylepšíte. Jak by měly články vypadat, popisují stránky Vzhled a styl a Encyklopedický styl. |
|
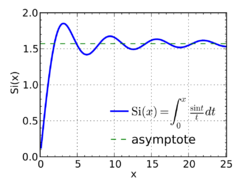
Integrálsinus je definován jako integrál
\(\operatorname{Si}\, x= \int_0^x \frac{\sin t}{t} dt = x - \frac{x^3}{3\cdot 3!}+\frac{x^5}{5\cdot 5!}-\frac{x^7}{7\cdot 7!}+\cdots\),
který není vyjádřitelný pomocí elementárních funkcí. Řada byla získána prostým integrováním mocninné řady pro \(\frac{\sin x}{x}\) člen po členu.
Z tvaru mocninné řady je zřejmé, že jde o funkci lichou. Pro \(x>0\) má extrémy v bodech \(n\pi\), kde \(n\) je přirozené číslo.
Přičemž lichým \(n\) odpovídají maxima a sudým minima.
Například pomocí reziduové věty lze vypočítat, že
\(\lim_{x\to \infty} \operatorname{Si}\, x = \int_0^{\infty}\frac{\sin t}{t} dt = \frac{\pi}{2}\)
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |