V sobotu 2. listopadu proběhla mohutná oslava naší plnoletosti !!
Multimediaexpo.cz je již 18 let na českém internetu !!

Komplexní číslo

Z Multimediaexpo.cz

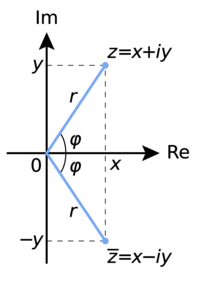
Znázornění komplexního čísla \(z = x + iy</math> a čísla k němu komplexně sdruženého \(\bar z = x - iy</math> v komplexní rovině. r je absolutní hodnota (norma).

Komplexní čísla (z latinského complexus, složený) vznikají rozšířením oboru reálných čísel tak, aby v něm každá algebraická rovnice měla příslušný počet řešení podle základní věty algebry. Například kvadratická rovnice x2 + 1 = 0 nemá v oboru reálných čísel řešení, protože její diskriminant (−4) je záporný a jeho odmocnina zde není definována. Komplexní číslo má dvě složky, reálnou a imaginární, a zapisuje se nejčastěji jako a + bi, přičemž i znamená imaginární jednotku, definovanou vztahem i2 = −1. Zmíněná rovnice pak má dvě řešení, ± i. Pro operace s komplexními čísly platí pravidla pro počítání s dvojčleny. Komplexní čísla lze interpretovat geometricky. Jako se reálná čísla zobrazují na reálné ose Re, budou imaginární čísla zobrazena na kolmé imaginární ose Im a každé komplexní číslo se zobrazí jako bod v rovině se souřadnicemi [x, y]. Číslo tvaru [x, 0] je reálné, číslo tvaru [0, y] je ryze imaginární. Absolutní hodnota komplexního čísla je pak vzdálenost bodu [x, y] od počátku souřadnic a číslo komplexně sdružené (tj. číslo [x, −y]) je zrcadlovým obrazem bodu [x, y] podle reálné osy Re. Komplexní čísla jsou významná nejen v matematice, ale také ve fyzice, zejména v elektrotechnice, v optice, v hydrodynamice i jinde.

Obsah

Zápis a související pojmy

Komplexním číslem nazveme číslo tvaru \( a + bi \,\! </math>, kde \( a \,\! </math> a \( b \,\! </math> jsou reálná čísla. Tento tvar komplexního čísla se nazývá algebraický. Písmeno \( i \,\! </math> značí imaginární jednotku, která se formálně zavádí jako číslo splňující rovnici \(i^2+1=0\,,</math> tj. jako odmocnina z −1, která v reálných číslech neexistuje. Elektrotechnici používají komplexní čísla velice často k výpočtu střídavých proudů obvodem, a protože přitom střídavý proud označují malým písmenem i, neoznačují imaginární jednotku písmenem i, ale písmenem j. Reálné číslo \( a \,\! </math> se nazývá reálnou částí tohoto komplexního čísla a číslo \( b \,\! </math> jeho imaginární částí. Pokud je \( b = 0 \,\! </math>, je dotyčné číslo reálným číslem \( a \,\! </math>, tj. reálná čísla tvoří podmnožinu čísel komplexních. Pokud je \( a = 0 \,\! </math>, mluvíme o ryze imaginárním číslu.

Značení

Potřebujeme-li pracovat pouze s reálnou, resp. imaginární částí komplexního čísla \(z \,\!</math>, používáme zápis \(a = \mathrm{Re}(z) = \Re(z)</math>, \(b = \mathrm{Im}(z) = \Im(z)</math>, kde \(a,b \,\!</math> jsou reálná čísla. Komplexní číslo \(z \,\!</math> lze tedy také vyjádřit některým z následujících zápisů \(z = a + \mathrm{i}b = \mathrm{Re}(z) + \mathrm{i} \mathrm{Im}(z) = \Re(z) + \mathrm{i} \Im(z) \,\!</math>. S imaginární jednotkou se zachází jako s každým jiným číslem, proto je možné používat následujících zkrácených zápisů:

  • \( 0 + x.i = x.i \,\! </math>
  • \( x + 0.i = x \,\! </math>
  • \( 1.i = i \,\! </math>
  • \( -1.i = -i \,\! </math>

Příklad

Číslo \( z = 3 + 2i \,\! </math> má reálnou část \( \mathrm{Re}(z) = 3 \,\!</math> a imaginární část \( \mathrm{Im}(z) = 2 \,\!</math>. Nejedná se ani o reálné, ani o ryze imaginární číslo.

Důvody pro zavedení komplexních čísel

Už perský matematik Al-Khwarizmi (asi 820) si všiml, že některé kvadratické rovnice nemají řešení. Italský matematik Girolamo Cardano (1501-1576) ukázal, že by stačilo vhodně definovat odmocninu záporného čísla, a René Descartes zavedl 1637 označení reálné a imaginární číslo. Zajímavé výsledky zkoumání těchto „neskutečných“ čísel ukázal Leonhard Euler a komplexní čísla přesně zavedl francouzský matematik Augustin Louis Cauchy (1821) a nezávisle na něm Carl Friedrich Gauss (1831). Obor reálných čísel, který vyjadřuje dostatečně dobře jakoukoliv kvantitu (množství), se tedy rozšiřuje do oboru komplexních čísel, jejichž význam není intuitivně příliš zřejmý, především proto, že v reálném oboru neleží řešení (kořeny) některých algebraických rovnic, čili obor reálných čísel není vzhledem k nim uzavřený. V oboru reálných čísel existují polynomy (s reálnými koeficienty a kladnými nezápornými celočíselnými exponenty), které nemají v oboru reálných čísel žádný kořen, případně je počet jejich reálných kořenů nižší, než stupeň polynomu. Obor komplexních čísel je uzavřený nejen na výše uvedené kořeny polynomů s reálnými koeficienty, ale i na kořeny polynomů s komplexními koeficienty. Tuto uzavřenost zaručuje Základní věta algebry, která tvrdí, že polynom n-tého stupně má v oboru komplexních čísel n kořenů.

Příklad

Polynom \( x^2 + 1 \,\! </math> nemá v oboru reálných čísel žádný kořen. V oboru komplexních čísel jsou jeho kořeny čísla \( i \,\! </math> a \( -i \,\! </math>, protože:

  • \( i^2 + 1 = -1 + 1 = 0 \,\! </math>
  • \( (-i)^2 + 1 = -1 + 1 = 0 \,\! </math>

Operace s komplexními čísly

Algebraický tvar komplexních čísel

Pro čísla v algebraickém tvaru lze jednoduchými algebraickými úpravami odvodit vztahy pro součet, rozdíl a součin dvou komplexních čísel:

  • \((a+ib)+(c+id)=(a+c)+i(b+d) \,\! </math>
  • \((a+ib)-(c+id)=(a-c)+i(b-d) \,\! </math>
  • \((a+ib)\cdot(c+id)=(ac-bd)+i(ad + bc) \,\! </math>

Podíl dvou komplexních čísel lze vyjádřit takto:

  • \( {a + ib \over c + id} = {(a + ib) (c - id) \over (c + i d) (c - i d)} = {(ac+bd) + i (bc-ad) \over c^2 + d^2} = \left({a c + b d \over c^2 + d^2}\right) + i \left( {b c - a d \over c^2 + d^2} \right). </math>

Pro komplexní číslo \(z=a+bi</math> je definována konjugace (komplexně sdružené číslo) \(\bar{z}:=a-bi</math>. Jejich součin \(z\bar{z}=a^2+b^2</math> je vždy reálný a nezáporný a je roven nule pouze když \(z=0</math>. Pak můžeme psát pro inverzi stručně \(z^{-1}=\bar{z}/(z\bar{z})</math> pro \(z\neq 0</math>. Norma komplexního čísla \(z</math> je definována jako \(|z|:=\sqrt{z\bar{z}}</math>. Platí, že pro libovolná komplexní čísla \(z,w</math> je \(|zw|=|z||w|</math>, t.j. norma součinu je součin norem.

Geometrické znázornění komplexních čísel

Komplexní čísla se zobrazují v komplexní (Gaussově) rovině jako body se souřadnicemi x,y; x je reálná část komplexního čísla, y imaginární část. Na ose x leží reálná čísla, ose y ryze imaginární čísla. Kombinací těchto dvou složek (reálné a imaginární) dostaneme množinu všech komplexních čísel, tj. Gaussova rovina.

Goniometrický tvar komplexních čísel

Každé komplexní číslo z různé od nuly je možné jednoznačně vyjádřit v goniometrickém tvaru. Pokud si v komplexní rovině zvolíme polární souřadnicový systém, vzdálenost od počátku označíme |z| (absolutní hodnota, také nazývaná norma nebo modul) a orientovaný úhel \(\phi = JOZ</math> (argument), kde J[1;0], O je počátkem soustavy a Z je obraz komplexního čísla a + bi se souřadnicemi Z[a;b], platí: \(z=|z|(\cos \varphi + i.\sin \varphi) \,</math>. Absolutní hodnotu z algebraického tvaru komplexního čísla \(z = a + bi</math> lze vyjádřit takto: \(|z| = \sqrt{ a^2 + b^2 }</math>.
Argument \(\varphi</math> lze vyjádřit ze vztahů: \(\cos \varphi = \frac{a}{|z|}</math>    a   \(\sin \varphi = \frac{b}{|z|}</math> Pro dělení komplexních čísel
\(z_1=|z_1|.(\cos \varphi_1 + i.\sin \varphi_1)</math> a
\(z_2=|z_2|.(\cos \varphi_2 + i.\sin \varphi_2)</math>
platí následující rovnice: \(\frac{z_1}{z_2}=\frac{|z_1|}{|z_2|}[\cos (\varphi_1 - \varphi_2) + i.\sin (\varphi_1 - \varphi_2)]</math> Pro násobení komplexních čísel z1 a z2 z předchozího příkladu slouží vzorec: \(z_1 . z_2=|z_1| . |z_2| . [\cos (\varphi_1 + \varphi_2) + i.\sin (\varphi_1 + \varphi_2)]</math> Pro n-tou mocninu komplexní čísla v goniometrickém tvaru platí tzv. Moivreova věta: \(z^n = |z|^n (\cos n\varphi + i\sin n\varphi) \,</math> Pro převod komplexních čísel z goniometrického tvaru na algebraický stačí zjistit hodnotu \(\cos \varphi</math> a \(\sin \varphi</math> a roznásobit závorku jako při práci s klasickým mnohočlenem.

Komplexní funkce reálné proměnné je funkce, jejímž definičním oborem jsou reálná čísla a oborem hodnot jsou komplexní čísla. Platí: h(x) = f(x) + ig(x) kde f je reálná část a g imaginární část komplexní funkce h. Obrazem takovéto funkce v Gaussově rovině je množina všech bodů X = [f(x),g(x)], kde x je z definičního oboru funkce. Při práci s komplexními čísly se také často využívá Eulerův vzorec.

Základní vlastnosti

Množina komplexních čísel se v matematice značí písmenem \(\mathbb{C}</math>. Komplexní čísla spolu se sčítáním, násobením a dělením tvoří těleso. Je to největší komutativní nadtěleso reálných čísel a taky je to algebraický uzávěr tělesa reálných čísel. Toto těleso nelze uspořádat. Komplexní čísla \(\mathbb{C}</math> je možno chápat jako dvoudimenzionální normovanou podílovou algebru nad \(\mathbb{R}</math>. Existují právě dva automorfizmy \(\mathbb{C}</math> jakožto algebry nad \(\mathbb{R}</math>: identita a konjugace. Je zajímavé, že existuje nekonečně mnoho automorfizmů \(\mathbb{C}</math> jako tělesa (ovšem jsou velmi nespojité a nezachovávají \(\mathbb{R}\subset\mathbb{C}</math>, což znamená, že reálná a čistě imaginární čísla nejsou určena samotnou strukturou tělesa \(\mathbb{C}</math> – porovnej s kvaterniony).

Definice pomocí uspořádaných dvojic

Často jsou také komplexní čísla zaváděna jako všechny uspořádané dvojice reálných čísel \( (a,b) </math> s definovanými operacemi sčítání a násobení: \((a,b)+(c,d)=(a+c,b+d) \,</math> \((a,b)\cdot(c,d)=(ac-bd,ad+bc)\,</math> Znaménko \(\cdot</math> u násobení obvykle vynecháváme. Množinu všech komplexních čísel obvykle značíme \(\mathbb C</math>. Číslo \((0,1)</math> pak nazveme imaginární jednotkou (zapisujeme \(i</math>). Pro číslo \(i</math> platí \(i^2=-1</math>. Použitím axiomů reálných čísel dostaneme následující tvrzení: \(\forall (a_1,a_2),(b_1,b_2),(c_1,c_2)\in{\mathbb C}:</math> 1. \((a_1,a_2)+(b_1,b_2)=(b_1,b_2)+(a_1,a_2)\,</math>
2. \((a_1,a_2)+\big((b_1,b_2)+(c_1,c_2)\big)=\big((a_1,a_2)+(b_1,b_2)\big)+(c_1,c_2)\,</math>
3. \((a_1,a_2)+(0,0)=(a_1,a_2)\,</math>
4. \((a_1,a_2)+(-a_1,-a_2)=(0,0)\,</math>
5. \((a_1,a_2)\cdot(b_1,b_2)=(b_1,b_2)\cdot(a_1,a_2)</math>
6. \((a_1,a_2)\cdot\big((b_1,b_2)\cdot(c_1,c_2)\big)=\big((a_1,a_2)\cdot(b_1,b_2)\big)\cdot(c_1,c_2)</math>
7. \((a_1,a_2)\cdot(1,0)=(a_1,a_2)</math>
8. \(\forall(a_1,a_2)\neq(0,0)\;(a_1,a_2)\cdot\left({a_1\over a_1^2+a_2^2},{-a_2\over a_1^2+a_2^2}\right)=(1,0)</math>
9. \((a_1,a_2)\cdot\big((b_1,b_2)+(c_1,c_2)\big)=(a_1,a_2)\cdot(b_1,b_2)+(a_1,a_2)\cdot(c_1,c_2)</math>

Související články

Reference

  • Prof. RNDr. Miloš Ráb, DrSc.: Komplexní čísla v elementární matematice, Masarykova univerzita, Brno, 1997, ISBN 80-210-1475-X

Externí odkazy


Citováno z „http://ww2000w.multimediaexpo.cz/mmecz/index.php/Komplexn%C3%AD_%C4%8D%C3%ADslo“