V sobotu 2. listopadu proběhla mohutná oslava naší plnoletosti !!
Multimediaexpo.cz je již 18 let na českém internetu !!
Multimediaexpo.cz je již 18 let na českém internetu !!
Dekerakt
Z Multimediaexpo.cz
(Rozdíly mezi verzemi)
m (1 revizi) |
(+ Masivní vylepšení) |
||
| Řádka 1: | Řádka 1: | ||
| - | {{ | + | {{upravit}} |
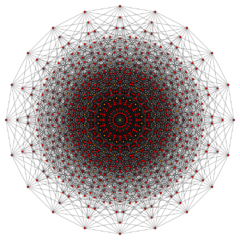
| + | [[Soubor:10-cube.png|thumb|240px|Dekerakt]] | ||
| + | V [[Geometrie|geometrii]] je '''dekerakt''' desetirozměrná [[analogie]] [[krychle]], jde tedy o speciální variantu [[nadkrychle]] pro d=10. Odborněji by mohl být dekerakt definován jako pravidelný [[konvexní čtyřúhelník]] s dvaceti eneraktovýmy 9 stěnami, 13 440 teseraktovými [[hypernadstěna]]mi a 15 360 krychlovými [[nadstěna]]mi. | ||
| + | ==Objem a obsah dekeraktu== | ||
| + | |||
| + | Tyto vzorce uvádějí obsah dekeraktu a jeho k-rozměrné povrchy. | ||
| + | |||
| + | ''V=a<sup>10</sup>'' | ||
| + | |||
| + | ''S<sub>9D</sub>=20 a<sup>9</sup>'' | ||
| + | |||
| + | ''S<sub>8D</sub>=180 a<sup>8</sup>'' | ||
| + | |||
| + | ''S<sub>7D</sub>=960 a<sub>7</sub>'' | ||
| + | |||
| + | ''S<sub>6D</sub>=3360 a<sup>6</sup>'' | ||
| + | |||
| + | ''S<sub>5D</sub>=8064 a<sup>5</sup>'' | ||
| + | |||
| + | ''S<sub>4D</sub>=13440 a<sup>4</sup>'' | ||
| + | |||
| + | ''S<sub>3D</sub>=15360 a<sup>3</sup>'' | ||
| + | |||
| + | ''S<sub>2D</sub>=11520 a<sup>2</sup>'' | ||
| + | |||
| + | ''S<sub>1D</sub>=5120 a'' | ||
| + | |||
| + | |||
| + | {{Polychora}}{{Článek z Wikipedie}} | ||
[[Kategorie:Geometrie]] | [[Kategorie:Geometrie]] | ||
[[Kategorie:Vícerozměrné geometrické útvary]] | [[Kategorie:Vícerozměrné geometrické útvary]] | ||
Aktuální verze z 4. 9. 2014, 07:46
V geometrii je dekerakt desetirozměrná analogie krychle, jde tedy o speciální variantu nadkrychle pro d=10. Odborněji by mohl být dekerakt definován jako pravidelný konvexní čtyřúhelník s dvaceti eneraktovýmy 9 stěnami, 13 440 teseraktovými hypernadstěnami a 15 360 krychlovými nadstěnami.
Objem a obsah dekeraktu
Tyto vzorce uvádějí obsah dekeraktu a jeho k-rozměrné povrchy.
V=a10
S9D=20 a9
S8D=180 a8
S7D=960 a7
S6D=3360 a6
S5D=8064 a5
S4D=13440 a4
S3D=15360 a3
S2D=11520 a2
S1D=5120 a
| VÍCEROZMĚRNÁ GEOMETRICKÁ TĚLESA | ||||
|---|---|---|---|---|
| d=2 | trojúhelník | čtverec | šestiúhelník | pětiúhelník |
| d=3 | tetraedr | krychle, oktaedr | krychloktaedr, kosočtverečný dvanáctistěn | dvanáctistěn , dvacetistěn |
| d=4 | 5-nadstěn | teserakt, 16-nadstěn | 24-nadstěn | 120-nadstěn, 600-nadstěn |
| d=5 | 5-simplex | penterakt, 5-ortoplex | ||
| d=6 | 6-simplex | hexerakt, 6-ortoplex | ||
| d=7 | 7-simplex | hepterakt, 7-ortoplex | ||
| d=8 | 8-simplex | okterakt, 8-ortoplex | ||
| d=9 | 9-simplex | ennerakt, 9-ortoplex | ||
| d=10 | 10-simplex | dekerakt, 10-ortoplex | ||
| d=11 | 11-simplex | hendekerakt, 11-ortoplex | ||
| d=12 | 12-simplex | dodekerakt, 12-ortoplex | ||
| d=13 | 13-simplex | triskaidekerakt, 13-ortoplex | ||
| d=14 | 14-simplex | tetradekerakt, 14-ortoplex | ||
| d=15 | 15-simplex | pentadekerakt, 15-ortoplex | ||
| d=16 | 16-simplex | hexadekerakt, 16-ortoplex | ||
| d=17 | 17-simplex | heptadekerakt, 17-ortoplex | ||
| d=18 | 18-simplex | oktadekerakt, 18-ortoplex | ||
| d=19 | 19-simplex | ennedekerakt, 19-ortoplex | ||
| d=20 | 20-simplex | ikosarakt, 20-ortoplex |
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |