Multimediaexpo.cz je již 18 let na českém internetu !!
Absolutně černé těleso
Z Multimediaexpo.cz
(+ Vylepšení) |
m (Nahrazení textu „<math>“ textem „<big>\(“) |
||
| Řádka 9: | Řádka 9: | ||
Maximum spektrální hustoty záření I(λ) je při jisté hodnotě λ(max), přičemž | Maximum spektrální hustoty záření I(λ) je při jisté hodnotě λ(max), přičemž | ||
| - | :< | + | :<big>\(\lambda_{max} = \frac{b}{T} </math> , ''b''=2.897 768 5(51) × 10<sup>–3</sup> m K |
Tento empirický vztah se nazývá ''Wienův posunovací zákon''. | Tento empirický vztah se nazývá ''Wienův posunovací zákon''. | ||
| Řádka 26: | Řádka 26: | ||
Německý fyzik [[Max Planck]] se zabýval problémem záření absolutně černého tělesa a uvažoval, že příčinou selhávání klasické teorie bude něco, co se pokládá za samozřejmé, ale nemusí to být pravdivé. Vyslovil [[hypotéza|hypotézu]], podle které si [[harmonický oscilátor]] může vyměňovat energii s okolím jen nespojitě po jistých kvantech. | Německý fyzik [[Max Planck]] se zabýval problémem záření absolutně černého tělesa a uvažoval, že příčinou selhávání klasické teorie bude něco, co se pokládá za samozřejmé, ale nemusí to být pravdivé. Vyslovil [[hypotéza|hypotézu]], podle které si [[harmonický oscilátor]] může vyměňovat energii s okolím jen nespojitě po jistých kvantech. | ||
| - | ::< | + | ::<big>\(\epsilon = h\nu</math> |
| - | kde < | + | kde <big>\(\nu</math> je frekvence oscilátoru a <big>\(h</math> je [[Planckova konstanta]], její hodnota je <big>\(h = 6,625 \cdot 10^{-34} \mathrm{Js}</math> |
Na základě představy, že těleso se skládá z velkého množství takovýchto oscilátorů, odvodil zákon záření absolutně černého tělesa, který se vyjadřuje například v některé z těchto podob: | Na základě představy, že těleso se skládá z velkého množství takovýchto oscilátorů, odvodil zákon záření absolutně černého tělesa, který se vyjadřuje například v některé z těchto podob: | ||
| - | ::< | + | ::<big>\(\mathrm{d}M_\mathrm{e} = \frac{2\pi hc^2}{\lambda^5} \frac{1}{e^{hc/\lambda kT}-1}\,\mathrm{d}\lambda\quad</math> ([[elektromagnetické spektrum|spektrum]] podle [[vlnová délka|vlnové délky]]),<ref>[http://alma.karlov.mff.cuni.cz/ufy102/Planckuv%20zakon.pdf Tepelné záření. Záření absolutně černého tělesa]. Rovnice 18. ''Učební text k přednášce UFY102''. Matematicko-fyzikální fakulta Univerzity Karlovy v Praze. Navštíveno 2013-10-05</ref> |
| - | ::< | + | ::<big>\(\mathrm{d}M_\mathrm{e} = \frac{2\pi h\nu^{3}}{c^2}\frac{1}{e^{{h\nu}/kT}-1}\,\mathrm{d}\nu\quad</math> (spektrum podle [[frekvence]]),<ref>[http://alma.karlov.mff.cuni.cz/ufy102/Planckuv%20zakon.pdf Tepelné záření. Záření absolutně černého tělesa]. Rovnice 21. ''Učební text k přednášce UFY102''. Matematicko-fyzikální fakulta Univerzity Karlovy v Praze. Navštíveno 2013-10-05</ref> |
| - | ::< | + | ::<big>\(\mathrm{d}M_\mathrm{e} = \frac{\hbar\omega^3}{4\pi^2 c^2}\frac{1}{e^{\hbar\omega/kT}-1}\,\mathrm{d}\omega\quad\,</math> (spektrum podle [[úhlová frekvence|úhlové frekvence]]), |
kde | kde | ||
| - | * < | + | * <big>\(\mathrm{d}M_\mathrm{e}</math> je [[intenzita vyzařování]] (tj. [[zářivý výkon]] jednotky [[povrch]]u) na vlnových délkách od <big>\(\lambda</math> do <big>\(\lambda + \mathrm{d}\lambda</math>, resp. na frekvencích od <big>\(\nu</math> do <big>\(\nu + \mathrm{d}\nu</math>, resp. na úhlových frekvencích od <big>\(\omega</math> do <big>\(\omega+\mathrm{d}\omega</math>, |
| - | * < | + | * <big>\(T</math> je [[teplota]] absolutně černého tělesa, |
| - | * < | + | * <big>\(h</math> je [[Planckova konstanta]], |
| - | * < | + | * <big>\(\hbar = h/2\pi</math> je redukovaná [[Planckova konstanta]] |
| - | * < | + | * <big>\(c</math> je [[rychlost světla]], |
| - | * < | + | * <big>\(k</math> je [[Boltzmannova konstanta]]. |
| - | Často se také uvádí vzorce pro [[zář]] < | + | Často se také uvádí vzorce pro [[zář]] <big>\(L_\mathrm{e}</math> ([[zářivý výkon]] jednotky [[povrch]]u do jednotky [[prostorový úhel|prostorového úhlu]]) namísto [[intenzita vyzařování|intenzity vyzařování]] <big>\(M_\mathrm{e}</math>. Jejich vzájemný vztah je <big>\(M_\mathrm{e} = \pi L_\mathrm{e}</math> díky tomu, že pro absolutně černé těleso je zář ve všech směrech stejná. |
=== Stefanův-Boltzmannův zákon === | === Stefanův-Boltzmannův zákon === | ||
''Hlavní článek: [[Stefanův-Boltzmannův zákon]]'' | ''Hlavní článek: [[Stefanův-Boltzmannův zákon]]'' | ||
| - | Celková [[intenzita vyzařování]] < | + | Celková [[intenzita vyzařování]] <big>\(M_\mathrm e</math> absolutně černého tělesa, tedy celkové množství energie vyzářené jednotkou plošného obsahu za jednotku času (ve [[watt]]ech na [[metr čtvereční]]), je úměrná čtvrté mocnině jeho teploty <big>\(T</math> (v [[kelvin]]ech): |
| - | :< | + | :<big>\(M_\mathrm e = \sigma T^4,</math> |
| - | kde < | + | kde <big>\(\sigma</math> je [[Stefanova-Boltzmannova konstanta]]. |
== Radiační teplota == | == Radiační teplota == | ||
Verze z 14. 8. 2022, 14:48
Absolutně černé těleso, černé těleso a nebo černý zářič je ideální těleso, které pohlcuje veškeré záření všech vlnových délek, dopadající na jeho povrch. Absolutně černé těleso je současně ideální zářič, ze všech možných těles o stejné teplotě vysílá největší možné množství zářivé energie. Celkové množství energie, které se vyzáří z povrchu absolutně černého tělesa za jednotku času a rozložení intenzity záření podle vlnových délek závisí jen na jeho teplotě. Záření Slunce se poměrně dobře blíží záření absolutně černého tělesa s teplotou přibližně 5800 Kelvinů, reliktní záření odpovídá záření absolutně černého tělesa s teplotou 2,7 K. Tento fyzikální pojem zavedl Gustav Kirchhoff v roce 1862.
Obsah |
Experimentální aproximace absolutně černého tělesa
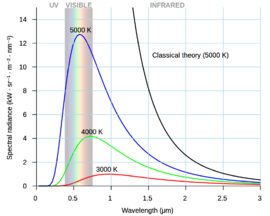
Schopnost tělesa vysílat elektromagnetické záření úzce souvisí s jeho schopností pohlcovat záření, protože těleso při konstantní teplotě je v termodynamické rovnováze se svým okolím, tedy získává pohlcováním energie od okolí stejné množství energie, jako do okolí vysílá. Absolutně černé těleso je možno aproximovat dutým tělesem s velmi malým otvorem. Všechno záření, které vniká do dutiny, zůstává v dutině a postupně je stěnami dutiny pohlcené. Stěny dutiny neustále vysílají a pohlcují záření. Záření, které z dutiny uniká přes malý otvor má vlastnosti blížící se záření absolutně černého tělesa. Experimentálně se zjistilo, že množství vyzářené energie závisí na teplotě a je tím větší, čím je teplota tělesa vyšší. Vysílané záření obsahuje elektromagnetické vlny různé vlnové délky a experimentálně se zjistilo, že množství energie záření s jistou vlnovou délkou se též mění. Množství vysílané energie se hodnotí pomocí spektrální hustoty záření I(λ), definované jako množství energie připadající na jednotkový interval vlnové délky. Pro všechny velikosti vlnové délky klesá k nule.
Wienův posunovací zákon
Maximum spektrální hustoty záření I(λ) je při jisté hodnotě λ(max), přičemž
- \(\lambda_{max} = \frac{b}{T} </math> , b=2.897 768 5(51) × 10–3 m K
Tento empirický vztah se nazývá Wienův posunovací zákon.
Zákon záření absolutně černého tělesa podle klasické fyziky
Ze zákonů klasické fyziky koncem 19. století Rayleigh a James Jeans odvodili zákon záření absolutně černého tělesa ve tvaru:
I(λ)dλ=8πkT/λ4 dλ
Tento vztah se nazývá Rayleighův-Jeansův zákon. Při snižovaní λ k hodnotám ultrafialové části spektra by I směrovalo k nekonečnu, což bylo v příkrém rozporu s experimenty. Tento nesoulad klasické teorie s experimentem se ve fyzikální literatuře nazýval ultrafialová katastrofa (modrá katastrofa) .
Kvantový zákon záření absolutně černého tělesa
- Související informace naleznete také v článku: Planckův vyzařovací zákon.
Německý fyzik Max Planck se zabýval problémem záření absolutně černého tělesa a uvažoval, že příčinou selhávání klasické teorie bude něco, co se pokládá za samozřejmé, ale nemusí to být pravdivé. Vyslovil hypotézu, podle které si harmonický oscilátor může vyměňovat energii s okolím jen nespojitě po jistých kvantech.
- \(\epsilon = h\nu</math>
kde \(\nu</math> je frekvence oscilátoru a \(h</math> je Planckova konstanta, její hodnota je \(h = 6,625 \cdot 10^{-34} \mathrm{Js}</math>
Na základě představy, že těleso se skládá z velkého množství takovýchto oscilátorů, odvodil zákon záření absolutně černého tělesa, který se vyjadřuje například v některé z těchto podob:
- \(\mathrm{d}M_\mathrm{e} = \frac{2\pi hc^2}{\lambda^5} \frac{1}{e^{hc/\lambda kT}-1}\,\mathrm{d}\lambda\quad</math> (spektrum podle vlnové délky),[1]
- \(\mathrm{d}M_\mathrm{e} = \frac{\hbar\omega^3}{4\pi^2 c^2}\frac{1}{e^{\hbar\omega/kT}-1}\,\mathrm{d}\omega\quad\,</math> (spektrum podle úhlové frekvence),
kde
- \(\mathrm{d}M_\mathrm{e}</math> je intenzita vyzařování (tj. zářivý výkon jednotky povrchu) na vlnových délkách od \(\lambda</math> do \(\lambda + \mathrm{d}\lambda</math>, resp. na frekvencích od \(\nu</math> do \(\nu + \mathrm{d}\nu</math>, resp. na úhlových frekvencích od \(\omega</math> do \(\omega+\mathrm{d}\omega</math>,
- \(T</math> je teplota absolutně černého tělesa,
- \(h</math> je Planckova konstanta,
- \(\hbar = h/2\pi</math> je redukovaná Planckova konstanta
- \(c</math> je rychlost světla,
- \(k</math> je Boltzmannova konstanta.
Často se také uvádí vzorce pro zář \(L_\mathrm{e}</math> (zářivý výkon jednotky povrchu do jednotky prostorového úhlu) namísto intenzity vyzařování \(M_\mathrm{e}</math>. Jejich vzájemný vztah je \(M_\mathrm{e} = \pi L_\mathrm{e}</math> díky tomu, že pro absolutně černé těleso je zář ve všech směrech stejná.
Stefanův-Boltzmannův zákon
Hlavní článek: Stefanův-Boltzmannův zákon
Celková intenzita vyzařování \(M_\mathrm e</math> absolutně černého tělesa, tedy celkové množství energie vyzářené jednotkou plošného obsahu za jednotku času (ve wattech na metr čtvereční), je úměrná čtvrté mocnině jeho teploty \(T</math> (v kelvinech):
- \(M_\mathrm e = \sigma T^4,</math>
kde \(\sigma</math> je Stefanova-Boltzmannova konstanta.
Radiační teplota
Taková teplota T absolutně černého tělesa, při které má hodnotu intenzity vyzařování HE0 stejnou jako intenzita vyzařování tělesa reálného HE .
Související články
Reference
- ↑ Tepelné záření. Záření absolutně černého tělesa. Rovnice 18. Učební text k přednášce UFY102. Matematicko-fyzikální fakulta Univerzity Karlovy v Praze. Navštíveno 2013-10-05
- ↑ Tepelné záření. Záření absolutně černého tělesa. Rovnice 21. Učební text k přednášce UFY102. Matematicko-fyzikální fakulta Univerzity Karlovy v Praze. Navštíveno 2013-10-05
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |
